1) The SUN
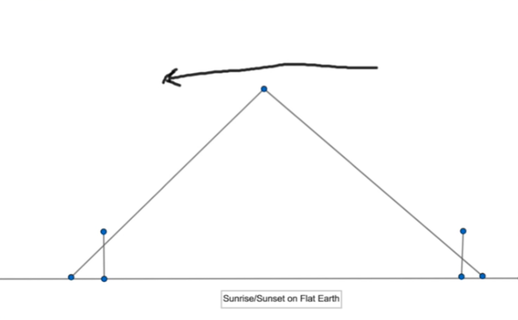
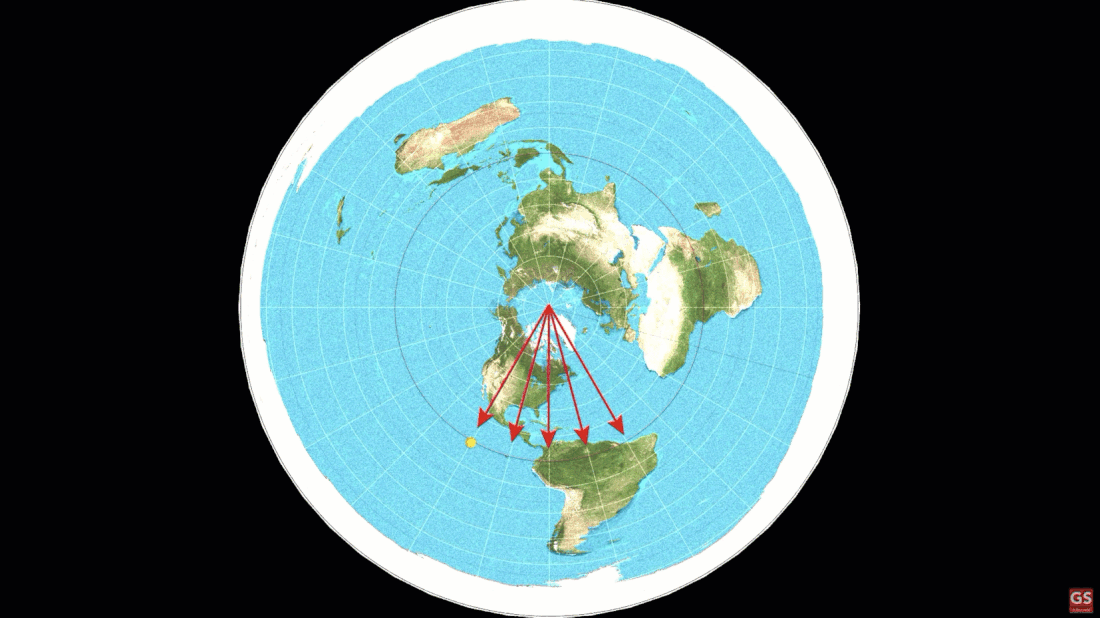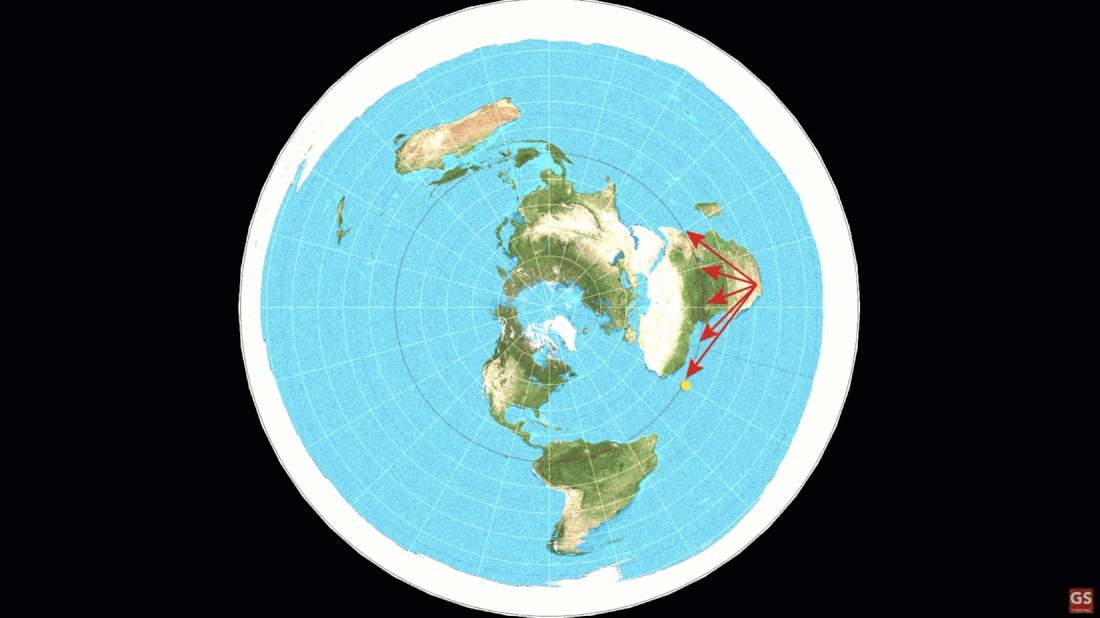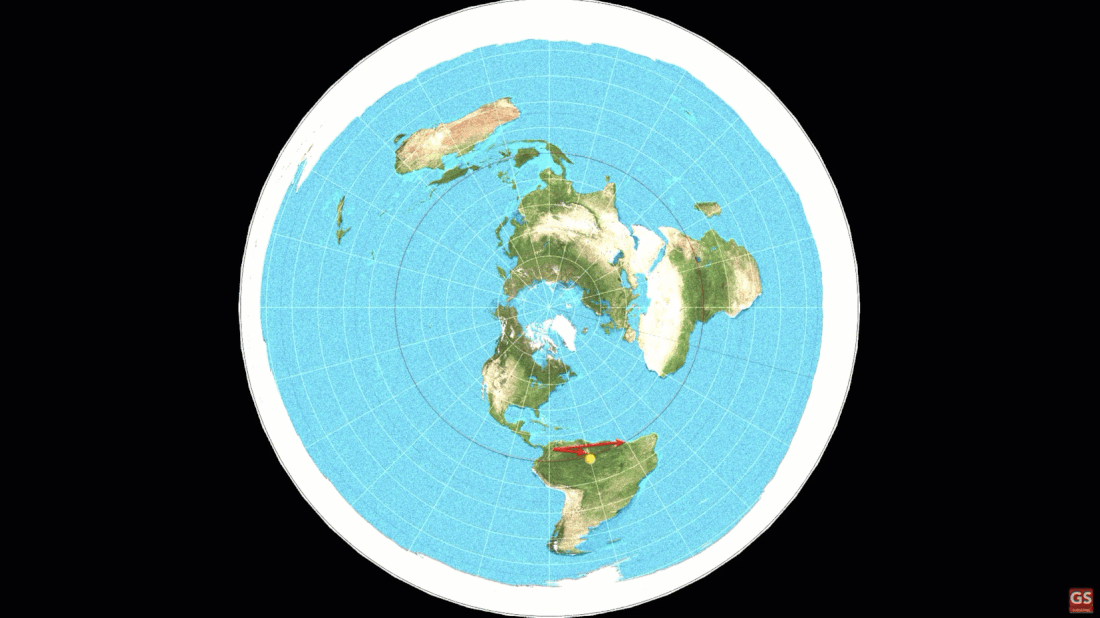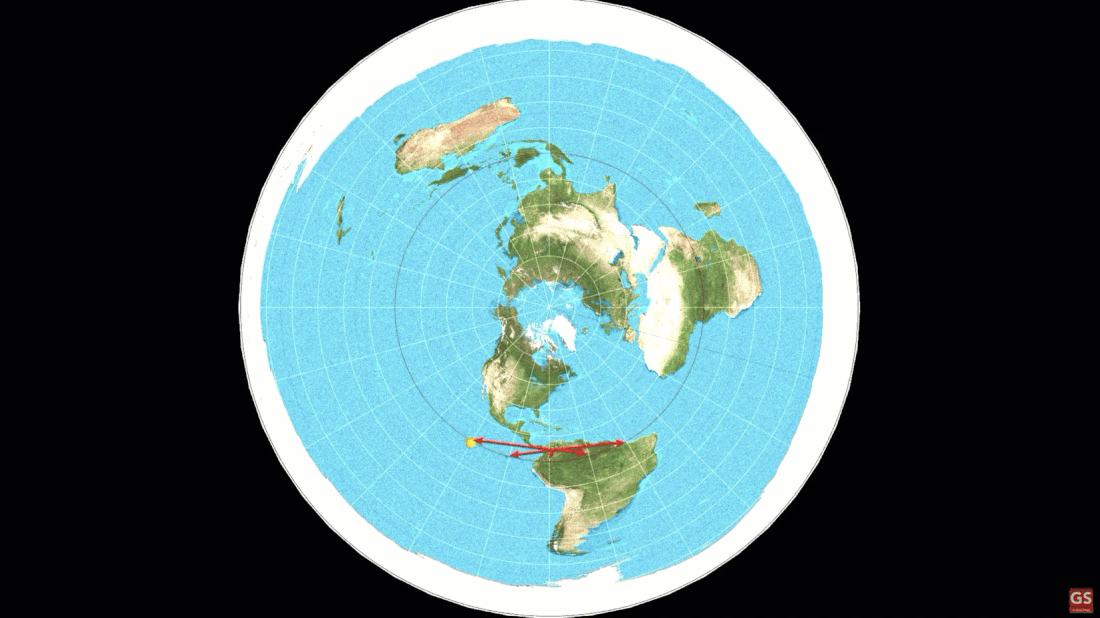
a. Top Down vs Bottom Up. Sun Lighting Mountains/Objects from Top down at sunrise, and staying lit at the top longest at sunset. Tip of a mountain first thing to light up and last thing to go dark.
a. Top Down vs Bottom Up. Sun Lighting Mountains/Objects from Top down at sunrise, and staying lit at the top longest at sunset. Tip of a mountain first thing to light up and last thing to go dark.
b. The suns location changes by 15 degrees every hour hour, every day, everywhere on the planet regardless of temperature or moisture content.
No Flat Earther Can Deny these points
1) 24 hour day / 360 degrees in a circle .....360 / 24 = 15 degree sections
2) Sun changes path on the plane of the ecliptic about
15 degrees each hour, no matter where you are on earth
Timeanddate.com you can see 15degree per hour anywhere on earth
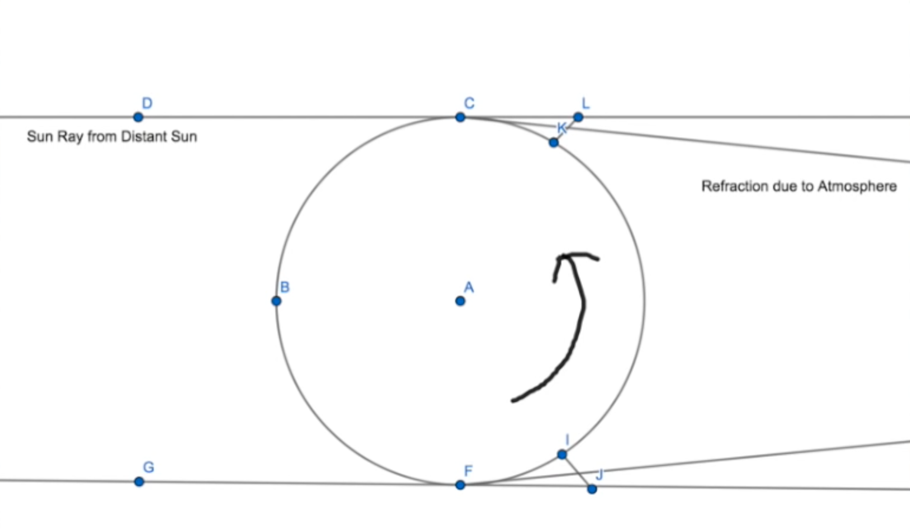
Because the sun is 93 million miles away, every location is essentially the same distance from the sun. Every place on earth is essentially the center of rotation.
The suns location changes by 15 degrees every hour hour, every day, everywhere on the planet regardless of temperature or moisture content. No amount of lensing or perspective could make that happen.
But you know what does make that happen?
A rotating earth and a distant sun!
No Flat Earther Can Deny these points
1) 24 hour day / 360 degrees in a circle .....360 / 24 = 15 degree sections
2) Sun changes path on the plane of the ecliptic about
15 degrees each hour, no matter where you are on earth
Timeanddate.com you can see 15degree per hour anywhere on earth
Because the sun is 93 million miles away, every location is essentially the same distance from the sun. Every place on earth is essentially the center of rotation.
The suns location changes by 15 degrees every hour hour, every day, everywhere on the planet regardless of temperature or moisture content. No amount of lensing or perspective could make that happen.
But you know what does make that happen?
A rotating earth and a distant sun!
2. The Stars -
A. Counter-rotating Star Fields
Star Trails - Center the camera on the North Star, keep the shutter open for a long exposure and watch the stars arc through the sky. They will trace a clockwise pattern all night long.
Celestial Equator - On the left we have a northern rotation in a clockwise direction and on the right we have a Southern rotation in a counterclockwise direction. In the middle we have stars going from the top, diagonally to the bottom and that is what is called the celestial equator.
A spherical earth spinning on its axis with a Northern and Southern Hemisphere perfectly explains these star trails, but think for a moment how could a dome over the surface of a flat and stationary earth possibly be constructed or rotate to give these two centers of rotation?
It's just not possible!
A. Counter-rotating Star Fields
Star Trails - Center the camera on the North Star, keep the shutter open for a long exposure and watch the stars arc through the sky. They will trace a clockwise pattern all night long.
Celestial Equator - On the left we have a northern rotation in a clockwise direction and on the right we have a Southern rotation in a counterclockwise direction. In the middle we have stars going from the top, diagonally to the bottom and that is what is called the celestial equator.
A spherical earth spinning on its axis with a Northern and Southern Hemisphere perfectly explains these star trails, but think for a moment how could a dome over the surface of a flat and stationary earth possibly be constructed or rotate to give these two centers of rotation?
It's just not possible!
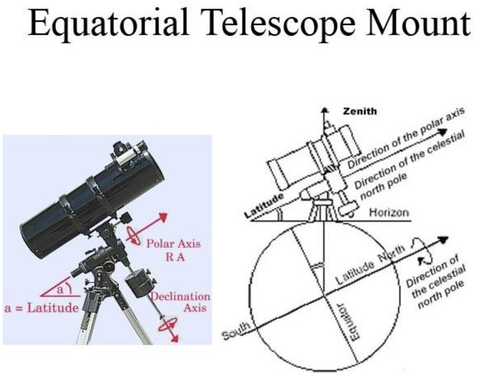
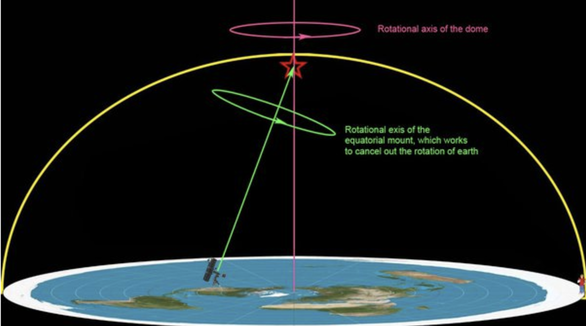
An equatorial mount is a telescope mount, where one axis is aligned parallel to the axis of rotation of earth (towards one of the celestial poles). Therefore a single axis movement can cancel out earth’s rotation to keep it pointed at any celestial object for a longer time. This is well proven to work. A flat earth with stars rotation concentric about the northern celestial pole would require always correction around two axes to track a star. The polar axis of an equatorial mount would always be not aligned with the celestial rotation of a flat earth. Therefore the fact, that an equatorial mount works perfectly, is in no way compatible with a flat earth. To maintain the notion, that earth is flat, one would have to deny the fact, that equatorial mounts work - which would be really hard to do, as thousands of people own telescopes with equatorial mounts - and they know, that they work.
Centrifugal Force and Why Things Weigh Less At the Equator vs the Poles
A
What about the effect of the spinning Earth? Near the equator, the acceleration is 0.0339 meter/sec2. Accelerometers do measure this force. But compared to gravity, it is small. Only 1/300 as large as gravity. Only scientific accelerometers are going to notice this. And they do notice it.
As Earth rotates, any object on its surface will feel a centrifugal force directed outward from the center of Earth and generally in the direction of local zenith. This causes Earth to be slightly bulged-out at the equator compared to the poles, which you can see from the difference between its equatorial radius of 6,378.14 km versus its polar radius of 6,356.75 km: a polar flattening difference of 21.4 kilometers. This centrifugal force also has an effect upon the local surface acceleration by reducing it slightly at the equator compared to the poles. At the equator, one would measure a value for ‘g’ that is about 9.78 m/sec2 while at the poles it is about 9.83 m/sec2
What about the effect of the spinning Earth? Near the equator, the acceleration is 0.0339 meter/sec2. Accelerometers do measure this force. But compared to gravity, it is small. Only 1/300 as large as gravity. Only scientific accelerometers are going to notice this. And they do notice it.
As Earth rotates, any object on its surface will feel a centrifugal force directed outward from the center of Earth and generally in the direction of local zenith. This causes Earth to be slightly bulged-out at the equator compared to the poles, which you can see from the difference between its equatorial radius of 6,378.14 km versus its polar radius of 6,356.75 km: a polar flattening difference of 21.4 kilometers. This centrifugal force also has an effect upon the local surface acceleration by reducing it slightly at the equator compared to the poles. At the equator, one would measure a value for ‘g’ that is about 9.78 m/sec2 while at the poles it is about 9.83 m/sec2
Tungsten is great because:
- It's not magnetic
- It will not absorb water or change weight by chemical reactions
- It's easy to carry around, as it's so dense.
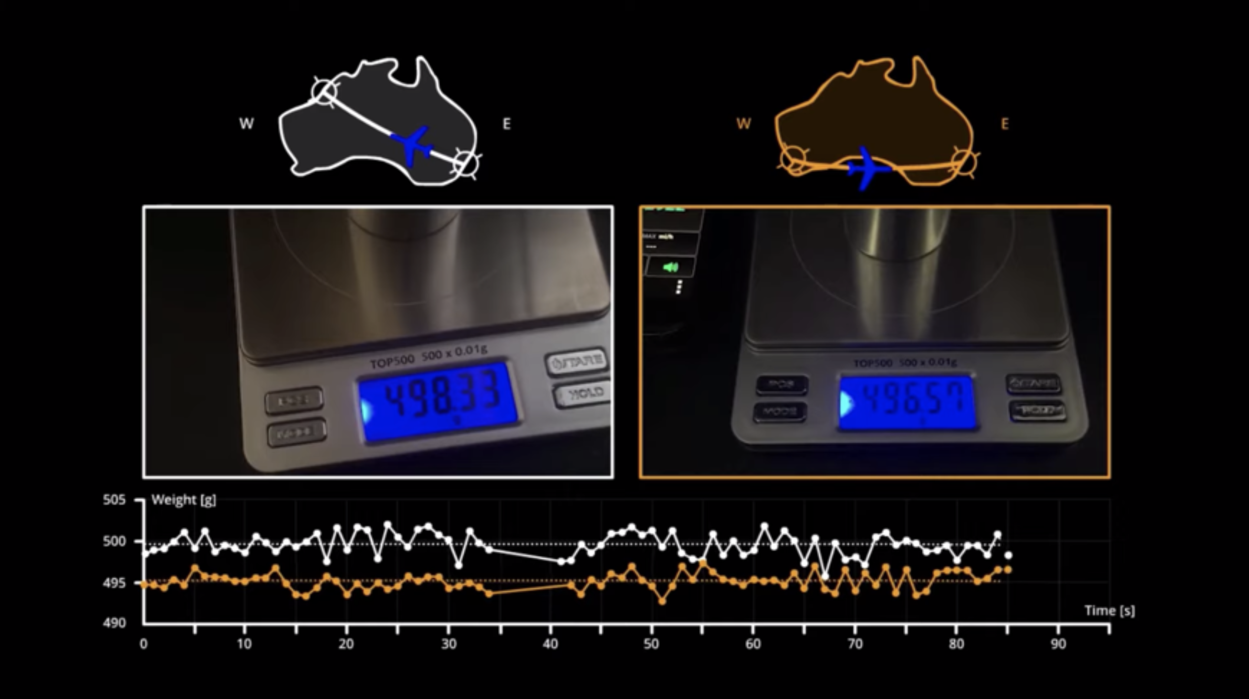
b. Eotvos Effect on East-West Flights - Weight Variation flying east or west (ut-vush)

Verifying Earth's rotation with the Eötvös effect. An experiment Flat Earthers are afraid to try.
Eötvös effect is the change in perceived gravitational acceleration when moving eastward vs. westward. An object will weigh slightly more when moving westward than when it is stationary or moving eastward.
The slight difference in weight due to the Eötvös effect can be measured in an experiment on a flight. The Eötvös effect is direct evidence that the Earth is a rotating sphere.
Eötvös effect is the change in perceived gravitational acceleration when moving eastward vs. westward. An object will weigh slightly more when moving westward than when it is stationary or moving eastward.
The slight difference in weight due to the Eötvös effect can be measured in an experiment on a flight. The Eötvös effect is direct evidence that the Earth is a rotating sphere.
4. Gyros - Earth Rotation and Axis (True North)
a. Optical - RLG esp
a. Optical - RLG esp
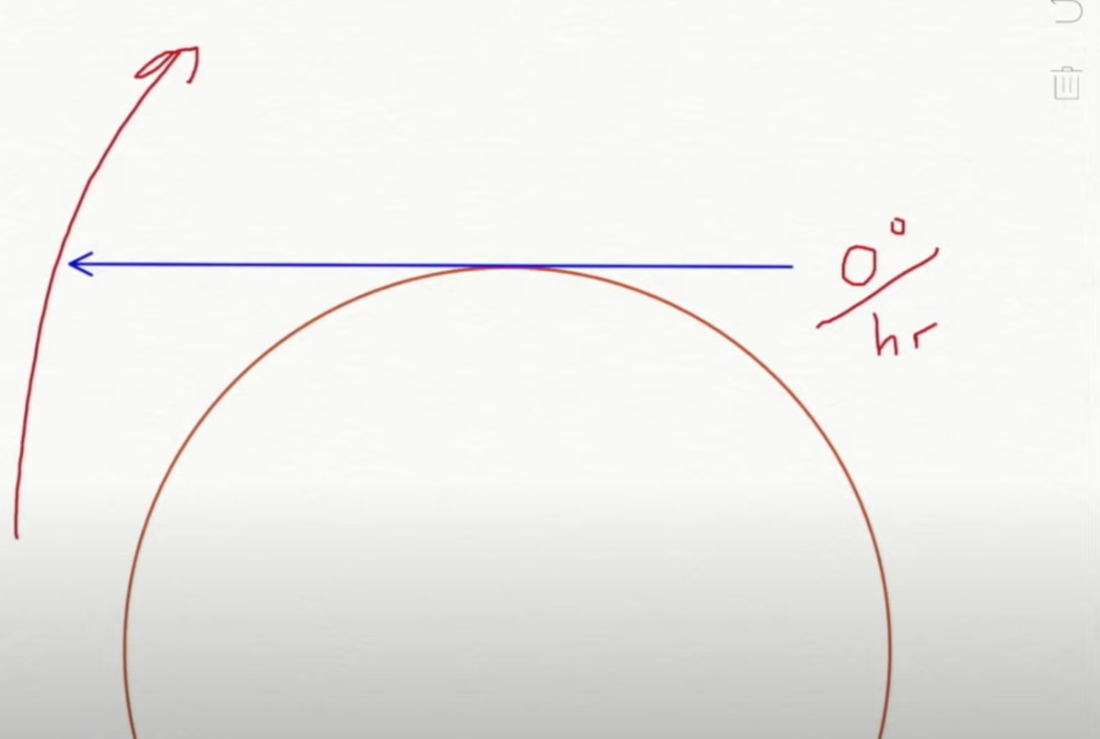
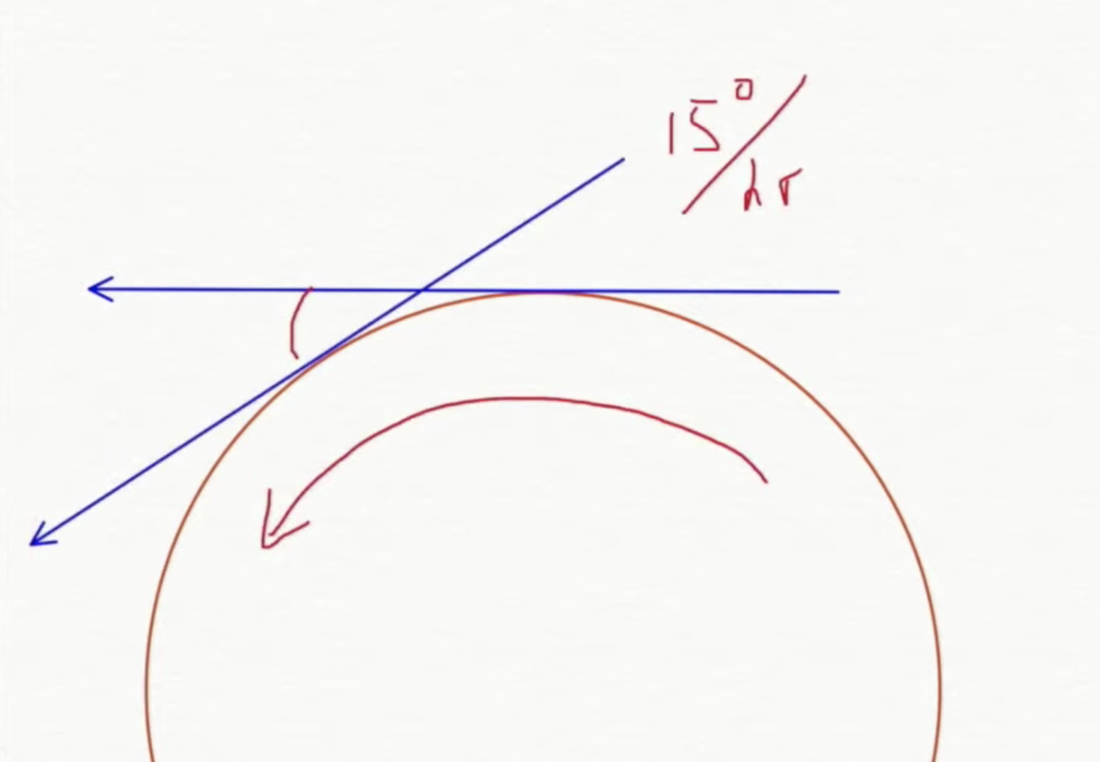
Ring Laser Gyroscope - This is the most convincing, and we have all seen Behind the Curve where Bob Knodel , a flat earth influencer proves FOR US that the earth is spinning. He basically debunks himself...lol... The 15 degree per hour drift he measures adds up to 24 hours for 360 degrees (One full earth rotation), which of course we all know is the length of a day.
As a physicist I can tell you they are INCREDIBLY accurate! THAT ALONE proves the earth is spinning, and Bob tried all kinds of tricks to get rid of the 15 degree per hour drift and he... FAILED!
There is no explanation on a stationary flat earth why an interferometric fiber optic would pick up a 15 degree per hour drift in 3 axis. It cannot be any kind of electromagnetic or electrostatic charge from the heaven energies because light does not have a charge and is therefore not affected by it.
As a physicist I can tell you they are INCREDIBLY accurate! THAT ALONE proves the earth is spinning, and Bob tried all kinds of tricks to get rid of the 15 degree per hour drift and he... FAILED!
There is no explanation on a stationary flat earth why an interferometric fiber optic would pick up a 15 degree per hour drift in 3 axis. It cannot be any kind of electromagnetic or electrostatic charge from the heaven energies because light does not have a charge and is therefore not affected by it.

Ring Laser Gyroscopes
Many tens of thousands of RLGs are operating in inertial navigation systems and have established high accuracy with better than .01 degree / hour bias uncertainty. 60,000 hours. No moving parts.
Inertial navigation - ships, planes, helicopters, ISS, submarines, missiles and satellites
Principle of operation - a certain rate of rotation induces a small difference between the time it takes light to traverse the ring in the two directions according to the sagnac effect. This induces a separation between the frequencies of the counter-propagating , a motion of the standing wave pattern within the ring, and thus a beat pattern. The net shift of that interference pattern follows the rotation of the unit in the plane of the ring.
Many tens of thousands of RLGs are operating in inertial navigation systems and have established high accuracy with better than .01 degree / hour bias uncertainty. 60,000 hours. No moving parts.
Inertial navigation - ships, planes, helicopters, ISS, submarines, missiles and satellites
Principle of operation - a certain rate of rotation induces a small difference between the time it takes light to traverse the ring in the two directions according to the sagnac effect. This induces a separation between the frequencies of the counter-propagating , a motion of the standing wave pattern within the ring, and thus a beat pattern. The net shift of that interference pattern follows the rotation of the unit in the plane of the ring.
b. Mechanical Gyros - Gyrocompasses especially
This is a marine gyrocompass. It does not rely on the magnetic poles of the earth to find true North. It uses the ROTATION of the earth and precesses until it points to true North. It has been put to use on thousands of ships the past 100 years or so where lives are at stake, so it HAS to work! It finds true North every time from any location on earth!! THIS FACT ALONE CONFIRMS WE ARE ON A SPINNING ROTATING PLANET!
This is a marine gyrocompass. It does not rely on the magnetic poles of the earth to find true North. It uses the ROTATION of the earth and precesses until it points to true North. It has been put to use on thousands of ships the past 100 years or so where lives are at stake, so it HAS to work! It finds true North every time from any location on earth!! THIS FACT ALONE CONFIRMS WE ARE ON A SPINNING ROTATING PLANET!
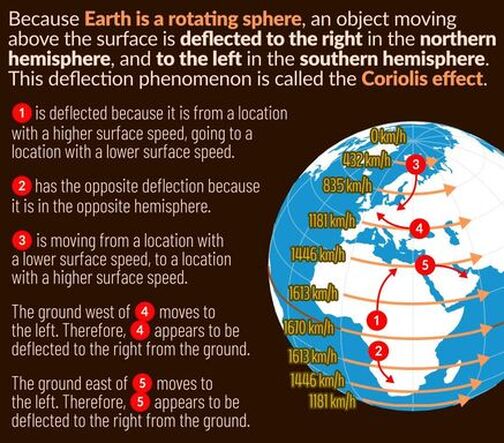
Coriolis
And if we are rotating there are certain effects that we should get, for instance the Coriolis force an apparent force caused by going from one area of the earth with a tangential velocity to one with less or more tangential velocity and this is all about the conservation of momentum.
And if we are rotating there are certain effects that we should get, for instance the Coriolis force an apparent force caused by going from one area of the earth with a tangential velocity to one with less or more tangential velocity and this is all about the conservation of momentum.
Coriolis Acceleration: The Coriolis acceleration exist only in the rotating reference frame of the earth. The Coriolis acceleration has 2 components, one acting horizontal perpendicular to the direction of motion in earths reference frame and one acting vertical. Coriolis Acceleration only displays the horizontal component of the Coriolis acceleration. The vertical component of the Coriolis effect is called the Eötvös effect, which has no influence on the flight path.
The Coriolis force is a force that acts on objects that are in motion within a rotating frame of reference. Because the Earth is a rotating sphere, an object traveling unattached to Earth’s surface is affected by the Coriolis force, depending on its speed and direction, as well as its latitude on Earth’s surface.
The rotating motion of the Earth causes the different parts of Earth’s surface to have different linear speeds, depending on its distance from the Earth’s rotational axis. An object moving from a location to another with a different linear speed will be affected by the Coriolis force because the motion of the object is now being observed from another location with a different linear speed/direction relative to Earth’s rotational axis.
Due to the Coriolis force, in the northern hemisphere, an object moving to the north will be deflected to the right because it is moving to a location with a slower linear speed from Earth’s rotation. An object traveling to the south will also be deflected to its right because it is moving to a location with a faster linear speed.
The Coriolis force is a force that acts on objects that are in motion within a rotating frame of reference. Because the Earth is a rotating sphere, an object traveling unattached to Earth’s surface is affected by the Coriolis force, depending on its speed and direction, as well as its latitude on Earth’s surface.
The rotating motion of the Earth causes the different parts of Earth’s surface to have different linear speeds, depending on its distance from the Earth’s rotational axis. An object moving from a location to another with a different linear speed will be affected by the Coriolis force because the motion of the object is now being observed from another location with a different linear speed/direction relative to Earth’s rotational axis.
Due to the Coriolis force, in the northern hemisphere, an object moving to the north will be deflected to the right because it is moving to a location with a slower linear speed from Earth’s rotation. An object traveling to the south will also be deflected to its right because it is moving to a location with a faster linear speed.
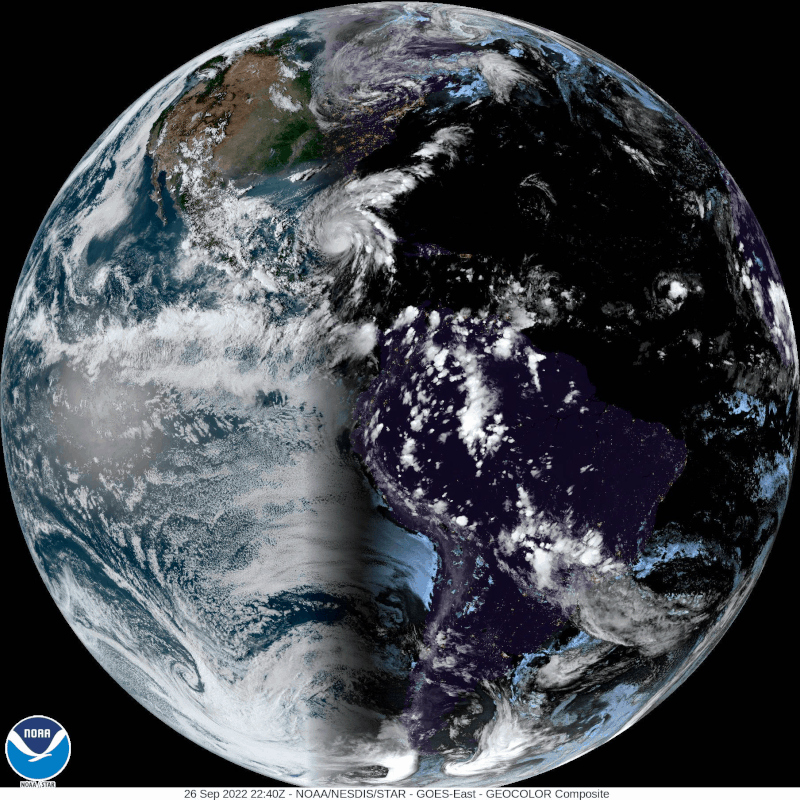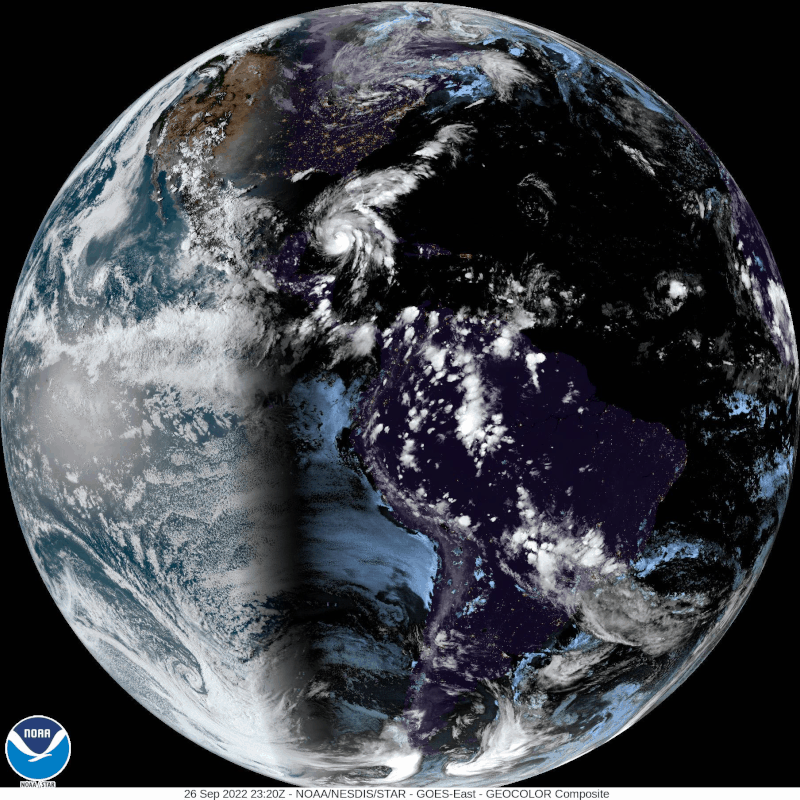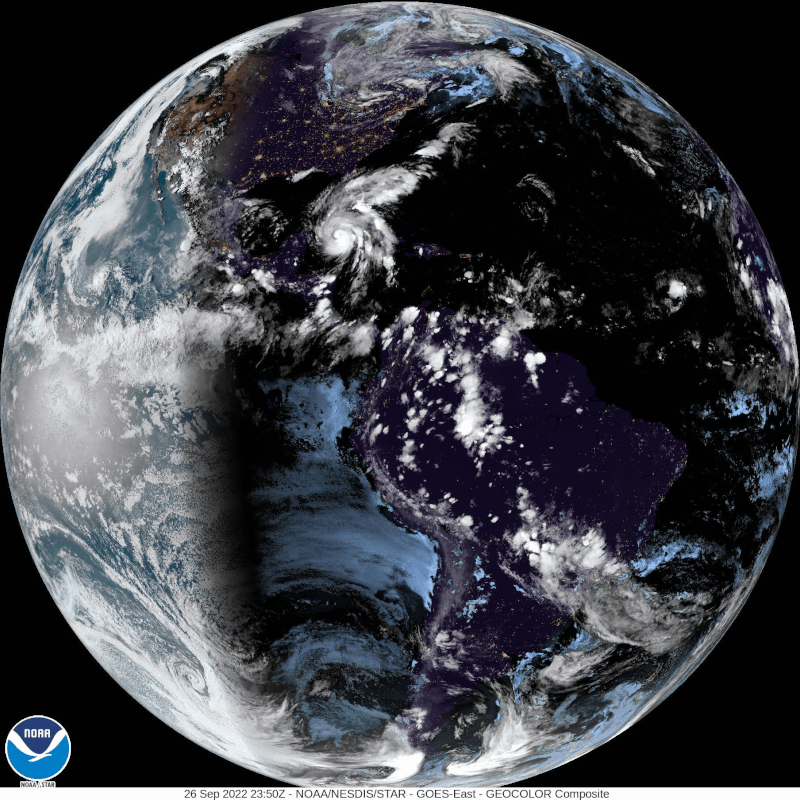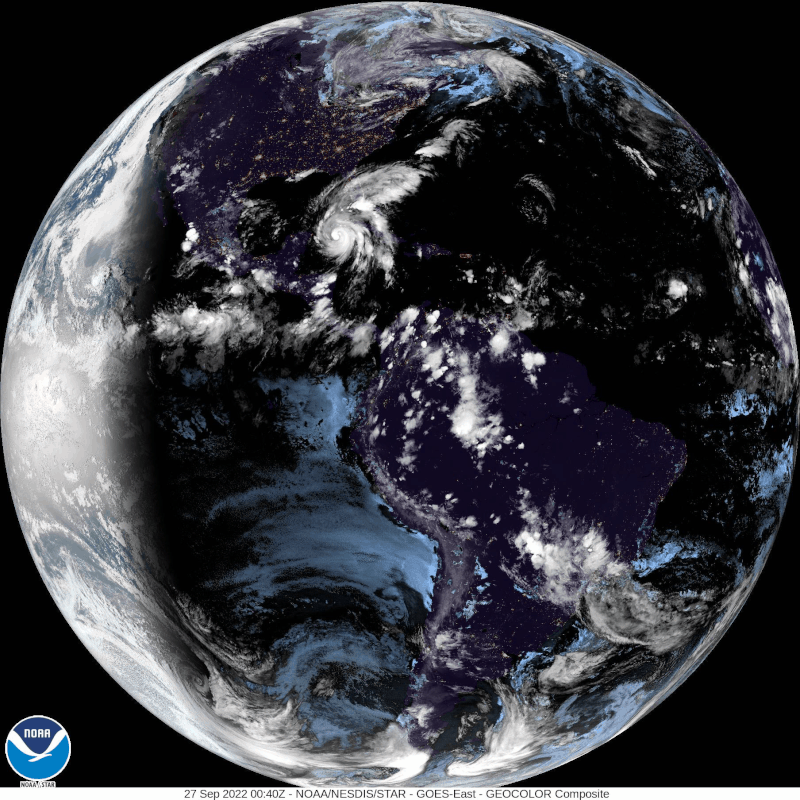
Hurricane Ian is rotating Counterclockwise BECAUSE the earth is spinning and the Coriolis Effect is VERY Real! If you live in Florida, like I do be prepared and be safe!
This is a very recent image of Hurricane Ian from GOES 16, and it is rotating as expected counterclockwise. And by the way, GOES is giving us proof like every 15 minutes the earth is a sphere with high resolution whole disk images!
A hurricane rotates in a different direction depending on which hemisphere it occurs. A cyclone rotates counterclockwise in the Northern Hemisphere, and clockwise in the Southern Hemisphere.
The phenomenon happens because of the Coriolis effect, which in turn occurs because the Earth is spherical and rotating. The tangential speed of the earth is faster at the equator than the poles which nudges the angular momentum of the hurricane to follow the Coriolis Force from the spinning earth which are mirror opposites in both hemispheres.
This fact also makes a hurricane happen very rarely near the equator. Near the equator, the Coriolis effect is too weak that it is almost impossible for a cyclone to form.
This phenomenon cannot possibly happen if the Earth is flat and motionless.
This is a very recent image of Hurricane Ian from GOES 16, and it is rotating as expected counterclockwise. And by the way, GOES is giving us proof like every 15 minutes the earth is a sphere with high resolution whole disk images!
A hurricane rotates in a different direction depending on which hemisphere it occurs. A cyclone rotates counterclockwise in the Northern Hemisphere, and clockwise in the Southern Hemisphere.
The phenomenon happens because of the Coriolis effect, which in turn occurs because the Earth is spherical and rotating. The tangential speed of the earth is faster at the equator than the poles which nudges the angular momentum of the hurricane to follow the Coriolis Force from the spinning earth which are mirror opposites in both hemispheres.
This fact also makes a hurricane happen very rarely near the equator. Near the equator, the Coriolis effect is too weak that it is almost impossible for a cyclone to form.
This phenomenon cannot possibly happen if the Earth is flat and motionless.
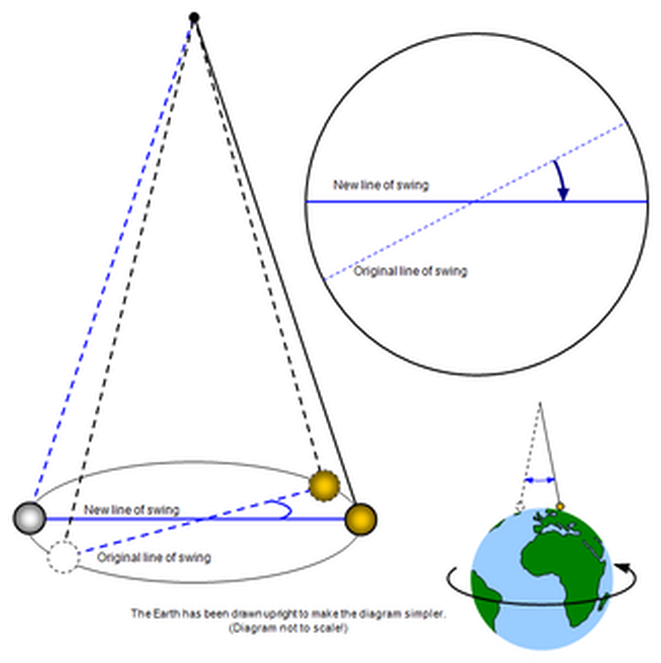
Foucault Pendulum -
Foucault’s pendulum proves Earth’s rotation. In the Northern Hemisphere, the pendulum rotates clockwise. In the Southern Hemisphere, it rotates counterclockwise. The pendulum turns faster if it is closer to the pole. On the Equator, the pendulum does not rotate.
Flat-Earthers invented various excuses to discredit Foucault’s pendulum. In reality, anyone not near the Equator can easily repeat the experiment, and it will give the expected result.
The Foucault pendulum will rotate with an angular velocity of 360° × sin φ per day, where φ is the latitude of the pendulum’s location. It rotates clockwise in the northern hemisphere and counterclockwise in the southern hemisphere. There is only one explanation for why Foucault’s pendulum behaves like that: the Earth is a rotating sphere.
You can accurately determine you latitude. This same Coriolis force cause a drift in a pendulum.
Gentlemen Physicsist
Foucault’s pendulum proves Earth’s rotation. In the Northern Hemisphere, the pendulum rotates clockwise. In the Southern Hemisphere, it rotates counterclockwise. The pendulum turns faster if it is closer to the pole. On the Equator, the pendulum does not rotate.
Flat-Earthers invented various excuses to discredit Foucault’s pendulum. In reality, anyone not near the Equator can easily repeat the experiment, and it will give the expected result.
The Foucault pendulum will rotate with an angular velocity of 360° × sin φ per day, where φ is the latitude of the pendulum’s location. It rotates clockwise in the northern hemisphere and counterclockwise in the southern hemisphere. There is only one explanation for why Foucault’s pendulum behaves like that: the Earth is a rotating sphere.
You can accurately determine you latitude. This same Coriolis force cause a drift in a pendulum.
Gentlemen Physicsist
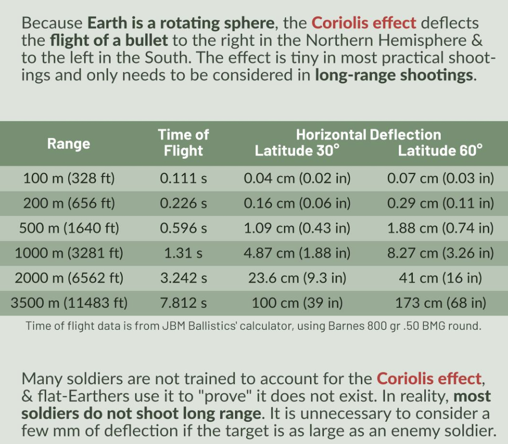
Flat Earthers will often claim that military ballistics doesn't need to take Earth curvature into account.
Ordnance Pamphlet No. 770 begs to differ:
Ordnance Pamphlet No. 770 begs to differ:
It is a myth to say Sinks, Bath Tubs and Toilets flow counterclockwise in the Northern Hemisphere and Clockwise in Southern Hemisphere... Or is it? These everyday systems DO actually experience the Coriolis Effect, however other forces acting on small basins (sinks, tubs, toilets, etc) will overwhelm the Coriolis Effect unless carefully controlled for. For example, your toilet has jets that will spray the water in a preferential direction.
But if you carefully control an experiment like the video below, you WILL see Coriolis just like in Huricanes, Foucault Pendulums, gyroscopes etc.
But if you carefully control an experiment like the video below, you WILL see Coriolis just like in Huricanes, Foucault Pendulums, gyroscopes etc.

The Runway Problem - flying from North Pole to Ecuador (6000 miles)
The needed bank angle for such a sideways acceleration is for any airplane the same: only a tiny 0.15°.
The thrust has to be increased only 0.00021 %. This has not to be taken into account in any calculations.
The plane must be accelerated to overcome the apparent Coriolis force. Otherwise the plane would appear to be drifting west at greater than the speed of sound.
The force that overcomes Coriolis in this case must come from the engines of the plane, though some of the force comes from atmospheric friction which tends to pull the plane in the direction of the Earth's rotation.
If you fired a cannon ball from the north pole toward the Equator, the cannon ball would appear to curve west. To continue south, it would have to acquire acceleration in an Easterly direction (viewed from an ECI reference frame.)
This is analogous to trying to roll a ball straight out from the center of a merry-go-round. In the rotating reference frame of the merry-go-round, the ball takes a curved path due to Coriolis forse. Without something to counteract Coriolis force, the ball cannot take a straight path.
Or image swimming across a river that has a current.
A cannonball does not magically lose its rotational momentum simply because you fire it upwards. The deflection of about inches is exactly what you would expect, and 2 feet is likely due to wind. Show me your math...
The needed bank angle for such a sideways acceleration is for any airplane the same: only a tiny 0.15°.
The thrust has to be increased only 0.00021 %. This has not to be taken into account in any calculations.
The plane must be accelerated to overcome the apparent Coriolis force. Otherwise the plane would appear to be drifting west at greater than the speed of sound.
The force that overcomes Coriolis in this case must come from the engines of the plane, though some of the force comes from atmospheric friction which tends to pull the plane in the direction of the Earth's rotation.
If you fired a cannon ball from the north pole toward the Equator, the cannon ball would appear to curve west. To continue south, it would have to acquire acceleration in an Easterly direction (viewed from an ECI reference frame.)
This is analogous to trying to roll a ball straight out from the center of a merry-go-round. In the rotating reference frame of the merry-go-round, the ball takes a curved path due to Coriolis forse. Without something to counteract Coriolis force, the ball cannot take a straight path.
Or image swimming across a river that has a current.
A cannonball does not magically lose its rotational momentum simply because you fire it upwards. The deflection of about inches is exactly what you would expect, and 2 feet is likely due to wind. Show me your math...
Note: The horizontal lift is used to counter the horizontal Coriolis force. It accelerates the airplane sideways exactly the amount necessary to keep up with the different tangential speeds of the surface of the earth with respect to space at different latitudes.
The Coriolis force acts always to the right in the northern hemisphere and to the left in the southern hemisphere. We can calculate the Coriolis acceleration instead of the Coriolis force. The connection is a = F / m. This way we get rid of the mass term m:
a(c) = 2*v*w*sin(0).
Note: as the airplane changes speed and latitude, the needed corrections constantly change and get smaller as the airplane approaches the equator, where the Coriolis effect is zero
http://walter.bislins.ch/bloge/index.asp?page=How+Airplanes+correct+for+the+Coriolis+Effect
The Coriolis force acts always to the right in the northern hemisphere and to the left in the southern hemisphere. We can calculate the Coriolis acceleration instead of the Coriolis force. The connection is a = F / m. This way we get rid of the mass term m:
a(c) = 2*v*w*sin(0).
Note: as the airplane changes speed and latitude, the needed corrections constantly change and get smaller as the airplane approaches the equator, where the Coriolis effect is zero
http://walter.bislins.ch/bloge/index.asp?page=How+Airplanes+correct+for+the+Coriolis+Effect

***NOTE: Planes don't have to constantly pitch down to fly. Actually they simply adjust their elevator trim for zero vertical speed and this automatically causes the plane to rotate to compensate for the curvature of the Earth.
Ok, so how much rotation are we talking about here? Surely the pilot would notice, right?
The Earth is ~3959 miles radius and there are 360 degrees in a full circle so that means we have approximately 360/(2*3959*pi) = 0.01447° per mile.
Let's say we're in a 747 going 500 mph, so the plane needs to rotate 500 * 0.01447° per hour, or 1/3600 of that per second
(360/(2*3959*pi))*500/60/60 = 0.00201°
So that's a constant VERY SLOW PITCH rate of 0.00201° per second or just 0.12° per minute.
But does the pilot actually has to keep pitching forward?
No. Again, you have to understand how aircraft work.
Planes control pitch using a control surface called the Elevator (usually on the trailing edge of the Horizontal Stabilizer)
And along the Elevator you'll find another smaller control surface called the Trim Tab.
Here is the most important point in this discussion:
The Elevator does not directly control the Pitch of the Airplane - it controls the RATE OF PITCH.
I think that Flat Earthers don't understand this concept.
https://flatearthinsanity.blogspot.com/2016/09/flat-earth-follies-planes-would-have-to.html
Ok, so how much rotation are we talking about here? Surely the pilot would notice, right?
The Earth is ~3959 miles radius and there are 360 degrees in a full circle so that means we have approximately 360/(2*3959*pi) = 0.01447° per mile.
Let's say we're in a 747 going 500 mph, so the plane needs to rotate 500 * 0.01447° per hour, or 1/3600 of that per second
(360/(2*3959*pi))*500/60/60 = 0.00201°
So that's a constant VERY SLOW PITCH rate of 0.00201° per second or just 0.12° per minute.
But does the pilot actually has to keep pitching forward?
No. Again, you have to understand how aircraft work.
Planes control pitch using a control surface called the Elevator (usually on the trailing edge of the Horizontal Stabilizer)
And along the Elevator you'll find another smaller control surface called the Trim Tab.
Here is the most important point in this discussion:
The Elevator does not directly control the Pitch of the Airplane - it controls the RATE OF PITCH.
I think that Flat Earthers don't understand this concept.
https://flatearthinsanity.blogspot.com/2016/09/flat-earth-follies-planes-would-have-to.html
A cannonball does not magically lose its rotational momentum simply because you fire it upwards. The deflection of about inches is exactly what you would expect, and 2 feet is likely due to wind. Show me your math...
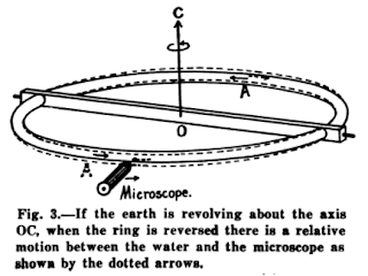
How Arthur Compton computed Latitude, direction to North, and length of a day
The apparatus is astonishingly simple - a round tube of water containing a mixture of coal oil and carbon tetrachloride of the same density as water in a constant temperature environment near freezing to minimize thermal influences and a microscope mounted for observing the motion of the fluid (one configuration projected the image on a screen). The tube was made more narrow at the point of observation as this amplifies the speed of the water moving past that point (the speeds in question are on the order of watching a minute hand on a watch move so proper care must be taken).
Here's the basic idea. The circular tube is filled with water and the tube is rotating along with the Earth. After some time, the rotational speed of the water will match the rotational speed of the tube and there will be no relative motion between the two. At this point, flip the tube over 180 degrees. The water will tend to keep rotating in the direction it was going in while the tube will now be moving in the opposite direction. By measuring the speed of the water, you get a measure of the Earth's rotational speed.
Big deal you say. A Foucault pendulum can give the same results you say. Well, as it turns out, it has a few drawbacks with respect to Compton's apparatus. Consider the case where either apparatus wasn't sitting at the Earth's pole. Then, you only get a measure of the Earth's rotation with respect to the axis of rotation perpendicular to the horizontal plane at your location. With a pendulum, you're done. You can show that the Earth is rotating, and knowing your location on the Earth, and making an assumption about the Earth's axis of rotation, you can determine how quickly the Earth is rotating. The annoying part, however, is making that assumption about the Earth's axis of rotation. With Compton's apparatus, you simply make two more measurements. Your second measurement is made with the plane of the ring perpendicular to the horizontal plane at your location. Then, you merely rotate the tube 90 degrees while still keeping it's plane perpendicular to horizontal. You now have three perpendicular components of the Earth's rotational speed and can re-construct both the Earth's total rotational speed and the direction of the axis of location.
American Physical Society's Physical Review article on Compton's apparatus
http://prola.aps.org.lib-ezproxy.tamu.edu:2048/abstract/PR/v5/i2/p109_1
DOI: 10.1103/PhysRev.5.109
The apparatus is astonishingly simple - a round tube of water containing a mixture of coal oil and carbon tetrachloride of the same density as water in a constant temperature environment near freezing to minimize thermal influences and a microscope mounted for observing the motion of the fluid (one configuration projected the image on a screen). The tube was made more narrow at the point of observation as this amplifies the speed of the water moving past that point (the speeds in question are on the order of watching a minute hand on a watch move so proper care must be taken).
Here's the basic idea. The circular tube is filled with water and the tube is rotating along with the Earth. After some time, the rotational speed of the water will match the rotational speed of the tube and there will be no relative motion between the two. At this point, flip the tube over 180 degrees. The water will tend to keep rotating in the direction it was going in while the tube will now be moving in the opposite direction. By measuring the speed of the water, you get a measure of the Earth's rotational speed.
Big deal you say. A Foucault pendulum can give the same results you say. Well, as it turns out, it has a few drawbacks with respect to Compton's apparatus. Consider the case where either apparatus wasn't sitting at the Earth's pole. Then, you only get a measure of the Earth's rotation with respect to the axis of rotation perpendicular to the horizontal plane at your location. With a pendulum, you're done. You can show that the Earth is rotating, and knowing your location on the Earth, and making an assumption about the Earth's axis of rotation, you can determine how quickly the Earth is rotating. The annoying part, however, is making that assumption about the Earth's axis of rotation. With Compton's apparatus, you simply make two more measurements. Your second measurement is made with the plane of the ring perpendicular to the horizontal plane at your location. Then, you merely rotate the tube 90 degrees while still keeping it's plane perpendicular to horizontal. You now have three perpendicular components of the Earth's rotational speed and can re-construct both the Earth's total rotational speed and the direction of the axis of location.
American Physical Society's Physical Review article on Compton's apparatus
http://prola.aps.org.lib-ezproxy.tamu.edu:2048/abstract/PR/v5/i2/p109_1
DOI: 10.1103/PhysRev.5.109

Spin
Airplanes DO correct for Corilois effect
Centrifual force exactly as a sphere predicts
Eötvös Effect: Direct Evidence Earth is a Rotating Sphere
Long-Range Snipers and the Coriolis & Eötvös Effects
Artillery
Ring Laser Gyroscope
The Foucault Pendulum Proves Spherical and Rotating Earth
Earth is an inertial reference frame
Explains precession
firing-vertically
Slow spin not fast, so perfectly works (angular speed vs tangential speed)
Bogus vortex model and relative speeds
Orbital spin explains seasons and why they are as long as they are
Orbital inclination and why we do not see eclipses every month
Keplers laws exact predict orbiting earth trajectory, change of speeds, etc.
Cyclonic Rotation: The Direction a Cyclone or Hurricane Rotates
Gyrocompass, Sagnac interferometer, Michelson-Gale-Pearson experiment, Compton
Airplanes DO correct for Corilois effect
Centrifual force exactly as a sphere predicts
Eötvös Effect: Direct Evidence Earth is a Rotating Sphere
Long-Range Snipers and the Coriolis & Eötvös Effects
Artillery
Ring Laser Gyroscope
The Foucault Pendulum Proves Spherical and Rotating Earth
Earth is an inertial reference frame
Explains precession
firing-vertically
Slow spin not fast, so perfectly works (angular speed vs tangential speed)
Bogus vortex model and relative speeds
Orbital spin explains seasons and why they are as long as they are
Orbital inclination and why we do not see eclipses every month
Keplers laws exact predict orbiting earth trajectory, change of speeds, etc.
Cyclonic Rotation: The Direction a Cyclone or Hurricane Rotates
Gyrocompass, Sagnac interferometer, Michelson-Gale-Pearson experiment, Compton
Hi Bryant
Can we find out that the earth orbits the sun, using only measurements on earth with no reference to celectial bodies?
Yes we can in principle, if we accept Newtons laws of motion and gravitation and that they work everywhere, only by measuring the tidal forces from the sun. Because this forces are very small and to get some accuracy we need to measure it to many decimal places, in practice this is not feasible.
The following description is the only method I can think of. Because motion is relative, i.e. the orbit of the earth is expressed with respect to the sun or the the fixed stars ect., how can we get the motion without referencing the sun or the stars in measurements? It's almost like asking a flat earther to calculate the relative density without allowing him to measure the density of the medium!
If we deny Newton's laws, we can not measure earths orbit around the sun only taking measurements on earth. But then we have to explain where the tides come from and how we can use Newtons laws to predict every motion on earth and where and why Newtons laws stop working.
Newtons law of gravitation predicts that celestial bodies attract each other according to:
F = G * M * m / d^2
F = forces between the bodies
G = gravitational constant
M, m = masses of the bodies
d = distance between the bodies
Because orbiting objects are in free fall around the common barycenter, this forces can not be measured in principle on the bodies itself. If the earth were fixed and the sun, with the mass we will calculate below, would orbit the earth, then we could measure this attractive force from the sun. It would be F/m = 0.00592962 m/s^2, which could easily be measured. We do not find such a force or acceleration, that means the earth is not fixed in space or the sun can not have a relevant mass.
But Newtons law of gravitation also predicts that there must also be tidal forces, if the sun and moon have some mass. We can observe tides which are synchronous with sun and moon, so sun and moon must have a rather big mass, depending on their distance. It turns out, that only by measuring the tidal forces on the near and far side on earth wrt. the sun we can calculate the distance between earth and sun only using Newtons law of gravitation:
Let's say the tidal force per kg, i.e. the acceleration, at the GP of the sun at noon is Fn (near) and on the opposite side of the earth Ff (far). Then we can calculate the distance to the sun:
d = 3R / 2 * (Fn + Ff) / (Fn - Ff) = 150.7e9 m (accepted value is 149.6e9 m)
d = distance to sun
R = 6,371,000 m = radius of earth
Fn = tidal force per kg (acceleration) on the GP of the sun, expected = 5.0508623e-7 N/kg
Ff = tidal force per kg (acceleration) on the opposite side, expected = 5.0502217e-7 N/kg
From the angular size of the sun of about 0.536° and the distance d we can calculate its diameter:
D = d * as * pi / 180° = 1.41e9 m (accepted value is 1.39e9 m)
D = diameter of the sun
d = 150.7e9 m = distance to the sun
as = 0.536° = mean angular size of the sun
We now have the distance to the sun, but don't know yet whether the earth orbits the sun or vice versa. To determine which is the case, we need the mass of the sun and the earth. The mass of the earth can be measured as follows:
m = R^2 * g / G = 5.97e24 kg (accepted value is 5.974e24 kg)
m = mass of the earth
R = 6,371,000 m = radius of the earth
g = 9.81 m/s^2 = gravitational acceleration on the surface of the earth
G = 6.674e-11 N * m^2 / kg^2 = gravitational constant(from Cavendish)
From the tidal forces and the distance to the sun we can calculate the mass of the sun:
M = Fn * d^3 / (G * 2R) = 2.03e30 kg (accepted value is 1.9884e30 kg)
M = mass of the sun
Fn = 5.0508623e-7 N/kg = expected tidal force per kg (acceleration) on the GP of the sun
d = 150.7e9 m = distance between earth and sun
G = 6.674e-11 N * m^2 / kg^2 = gravitational constant(from Cavendish)
R = 6,371,000 m = radius of the earth
Note: this equations are good approximations if d is much greater than R.
Because we can observe that the distance d is constant, following from Newtons law of gravitation we can derive that the sun and earth must orbit a common center, the barycenter. The barycenter lies on the line between earth and sun. It is always located nearer the more massive body. As we have calculated that the mass of the sun is about 340,000 times bigger than the mass of the earth, we know that the barycenter lies much closer to the center of the sun than to the earth. We can calculate the distance b of the barycenter from the center of the sun:
b = d * m / (M + m) = 443 km
b = distance of the barycenter from the center of the sun
d = 150.7e9 m = distance between earth and sun
m = 5.97e24 kg = mass of the earth
M = 2.03e30 kg = mass of the sun
As we can see, the barycenter lies within the sun. That means the earth effectively orbits the sun. We can even calculate the orbital period without any reference to the outside:
T = 2pi * sqrt( d^3 / GM ) = 365.5 days
Conclusion: Only using measurements made on earth I could calculate the distance to the sun, its mass, its size, that the barycenter lies within the sun, i.e. the earth orbits the sun, and the orbital period of the earth. No reference to the outside needed. Only Newtons laws applied.
Of course we have many other methods to confirm this finding. The measurable precession and nutation (using ring laser gyros) of earths axis is caused by sun, moon, the other planets and the rotation of the earth (-> ellipsoidal shape). Aberration, parallax, red shift, radar; all yield the same orbital parameters. We have sent probes to the sun, moon and all planets. The trajectories are calculated using Newtons laws and it works. We constantly measure the directions and distances to the satellites. There is of course no doubt, that the earth orbits the sun and not the other way around.
Walter
Can we find out that the earth orbits the sun, using only measurements on earth with no reference to celectial bodies?
Yes we can in principle, if we accept Newtons laws of motion and gravitation and that they work everywhere, only by measuring the tidal forces from the sun. Because this forces are very small and to get some accuracy we need to measure it to many decimal places, in practice this is not feasible.
The following description is the only method I can think of. Because motion is relative, i.e. the orbit of the earth is expressed with respect to the sun or the the fixed stars ect., how can we get the motion without referencing the sun or the stars in measurements? It's almost like asking a flat earther to calculate the relative density without allowing him to measure the density of the medium!
If we deny Newton's laws, we can not measure earths orbit around the sun only taking measurements on earth. But then we have to explain where the tides come from and how we can use Newtons laws to predict every motion on earth and where and why Newtons laws stop working.
Newtons law of gravitation predicts that celestial bodies attract each other according to:
F = G * M * m / d^2
F = forces between the bodies
G = gravitational constant
M, m = masses of the bodies
d = distance between the bodies
Because orbiting objects are in free fall around the common barycenter, this forces can not be measured in principle on the bodies itself. If the earth were fixed and the sun, with the mass we will calculate below, would orbit the earth, then we could measure this attractive force from the sun. It would be F/m = 0.00592962 m/s^2, which could easily be measured. We do not find such a force or acceleration, that means the earth is not fixed in space or the sun can not have a relevant mass.
But Newtons law of gravitation also predicts that there must also be tidal forces, if the sun and moon have some mass. We can observe tides which are synchronous with sun and moon, so sun and moon must have a rather big mass, depending on their distance. It turns out, that only by measuring the tidal forces on the near and far side on earth wrt. the sun we can calculate the distance between earth and sun only using Newtons law of gravitation:
Let's say the tidal force per kg, i.e. the acceleration, at the GP of the sun at noon is Fn (near) and on the opposite side of the earth Ff (far). Then we can calculate the distance to the sun:
d = 3R / 2 * (Fn + Ff) / (Fn - Ff) = 150.7e9 m (accepted value is 149.6e9 m)
d = distance to sun
R = 6,371,000 m = radius of earth
Fn = tidal force per kg (acceleration) on the GP of the sun, expected = 5.0508623e-7 N/kg
Ff = tidal force per kg (acceleration) on the opposite side, expected = 5.0502217e-7 N/kg
From the angular size of the sun of about 0.536° and the distance d we can calculate its diameter:
D = d * as * pi / 180° = 1.41e9 m (accepted value is 1.39e9 m)
D = diameter of the sun
d = 150.7e9 m = distance to the sun
as = 0.536° = mean angular size of the sun
We now have the distance to the sun, but don't know yet whether the earth orbits the sun or vice versa. To determine which is the case, we need the mass of the sun and the earth. The mass of the earth can be measured as follows:
m = R^2 * g / G = 5.97e24 kg (accepted value is 5.974e24 kg)
m = mass of the earth
R = 6,371,000 m = radius of the earth
g = 9.81 m/s^2 = gravitational acceleration on the surface of the earth
G = 6.674e-11 N * m^2 / kg^2 = gravitational constant(from Cavendish)
From the tidal forces and the distance to the sun we can calculate the mass of the sun:
M = Fn * d^3 / (G * 2R) = 2.03e30 kg (accepted value is 1.9884e30 kg)
M = mass of the sun
Fn = 5.0508623e-7 N/kg = expected tidal force per kg (acceleration) on the GP of the sun
d = 150.7e9 m = distance between earth and sun
G = 6.674e-11 N * m^2 / kg^2 = gravitational constant(from Cavendish)
R = 6,371,000 m = radius of the earth
Note: this equations are good approximations if d is much greater than R.
Because we can observe that the distance d is constant, following from Newtons law of gravitation we can derive that the sun and earth must orbit a common center, the barycenter. The barycenter lies on the line between earth and sun. It is always located nearer the more massive body. As we have calculated that the mass of the sun is about 340,000 times bigger than the mass of the earth, we know that the barycenter lies much closer to the center of the sun than to the earth. We can calculate the distance b of the barycenter from the center of the sun:
b = d * m / (M + m) = 443 km
b = distance of the barycenter from the center of the sun
d = 150.7e9 m = distance between earth and sun
m = 5.97e24 kg = mass of the earth
M = 2.03e30 kg = mass of the sun
As we can see, the barycenter lies within the sun. That means the earth effectively orbits the sun. We can even calculate the orbital period without any reference to the outside:
T = 2pi * sqrt( d^3 / GM ) = 365.5 days
Conclusion: Only using measurements made on earth I could calculate the distance to the sun, its mass, its size, that the barycenter lies within the sun, i.e. the earth orbits the sun, and the orbital period of the earth. No reference to the outside needed. Only Newtons laws applied.
Of course we have many other methods to confirm this finding. The measurable precession and nutation (using ring laser gyros) of earths axis is caused by sun, moon, the other planets and the rotation of the earth (-> ellipsoidal shape). Aberration, parallax, red shift, radar; all yield the same orbital parameters. We have sent probes to the sun, moon and all planets. The trajectories are calculated using Newtons laws and it works. We constantly measure the directions and distances to the satellites. There is of course no doubt, that the earth orbits the sun and not the other way around.
Walter