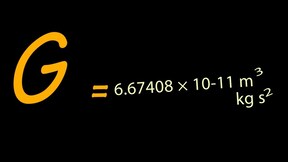
The gravitational constant (also known as the universal gravitational constant, the Newtonian constant of gravitation, or the Cavendish gravitational constant),[a] denoted by the capital letter G, is an empirical physical constant involved in the calculation of gravitational effects in Sir Isaac Newton's law of universal gravitation and in Albert Einstein's theory of general relativity.
In Newton's law, it is the proportionality constant connecting the gravitational force between two bodies with the product of their masses and the inverse square of their distance. In the Einstein field equations, it quantifies the relation between the geometry of spacetime and the energy–momentum tensor (also referred to as the stress–energy tensor).
The measured value of the constant is known with some certainty to four significant digits. In SI units, its value is approximately 6.674×10−11 m3⋅kg−1⋅s−2.
The modern notation of Newton's law involving G was introduced in the 1890s by C. V. Boys. The first implicit measurement with an accuracy within about 1% is attributed to Henry Cavendish in a 1798 experiment.
In Newton's law, it is the proportionality constant connecting the gravitational force between two bodies with the product of their masses and the inverse square of their distance. In the Einstein field equations, it quantifies the relation between the geometry of spacetime and the energy–momentum tensor (also referred to as the stress–energy tensor).
The measured value of the constant is known with some certainty to four significant digits. In SI units, its value is approximately 6.674×10−11 m3⋅kg−1⋅s−2.
The modern notation of Newton's law involving G was introduced in the 1890s by C. V. Boys. The first implicit measurement with an accuracy within about 1% is attributed to Henry Cavendish in a 1798 experiment.

The Man Who Weighed the Earth
Newton's Problem: Calculating G
Newton came up with F=Gm1*m2/r^2 for objects on earth but the force of gravity is so tiny that directly measuring the force between two known masses was beyond his experimental capabilities. Surprisingly, however, he was able to show that his formula, to a good degree of precision, accounted for the motion of the Moon around the Earth, as well as the attraction of the Earth on ordinary objects—the equivalence of the orbit of the Moon to the fall of the apple.
The issue for Newton
He could calculate the product of the constant G and the mass of the Earth, but without knowing one, he could not calculate the other. With large objects, like the planet Earth, the forces are easy to measure directly, so substituting the mass of the Earth and, say, an apple, he’d have this:
F=Gm*Me/R^2
Now, he could easily measure the weight and mass the apple, giving 𝐹𝑔 and 𝑚𝑎 , and the radius of the Earth was well known since the ancient Greeks measured it using shadows. But he had no way to know the mass of the Earth. You can’t just throw a planet on a balance and read its mass. So the best he could solve for was:
GMe = F*R^2/m
He could calculate the product of the constant G and the mass of the Earth (Me), but without knowing one, he could not calculate the other.
Not until Henry Cavendish, a brilliant experimentalist, was able to directly and accurately measure the incredibly tiny forces between some hefty lead spheres, could the two values be resolved, and a value for both the gravitational constant and the mass of the Earth be calculated.
You would think that Cavendish would be proud to be known as the man who discovered this fundamental physical constant, but he always preferred to be known by the somewhat catchier phrase: the “Man who Weighed the Earth”
Newton's Problem: Calculating G
Newton came up with F=Gm1*m2/r^2 for objects on earth but the force of gravity is so tiny that directly measuring the force between two known masses was beyond his experimental capabilities. Surprisingly, however, he was able to show that his formula, to a good degree of precision, accounted for the motion of the Moon around the Earth, as well as the attraction of the Earth on ordinary objects—the equivalence of the orbit of the Moon to the fall of the apple.
The issue for Newton
He could calculate the product of the constant G and the mass of the Earth, but without knowing one, he could not calculate the other. With large objects, like the planet Earth, the forces are easy to measure directly, so substituting the mass of the Earth and, say, an apple, he’d have this:
F=Gm*Me/R^2
Now, he could easily measure the weight and mass the apple, giving 𝐹𝑔 and 𝑚𝑎 , and the radius of the Earth was well known since the ancient Greeks measured it using shadows. But he had no way to know the mass of the Earth. You can’t just throw a planet on a balance and read its mass. So the best he could solve for was:
GMe = F*R^2/m
He could calculate the product of the constant G and the mass of the Earth (Me), but without knowing one, he could not calculate the other.
Not until Henry Cavendish, a brilliant experimentalist, was able to directly and accurately measure the incredibly tiny forces between some hefty lead spheres, could the two values be resolved, and a value for both the gravitational constant and the mass of the Earth be calculated.
You would think that Cavendish would be proud to be known as the man who discovered this fundamental physical constant, but he always preferred to be known by the somewhat catchier phrase: the “Man who Weighed the Earth”
- 0) The Original! Experiments to determine the Density of the Earth
- The value of G is incredibly important because of its key role in fields such as gravitation, cosmology, particle physics, geophysics and astrophysics. The first G value, with an uncertainty of about 1%, was obtained from Cavendish and Michell’s torsion pendulum experiment in 1798.
- Henry Cavendish, Esq. F.iR. S. and A. S.
- June 21, 1798
- https://www.jstor.org/stable/pdf/106988.pdf
- Direct PDF Download
- The value of G is incredibly important because of its key role in fields such as gravitation, cosmology, particle physics, geophysics and astrophysics. The first G value, with an uncertainty of about 1%, was obtained from Cavendish and Michell’s torsion pendulum experiment in 1798.
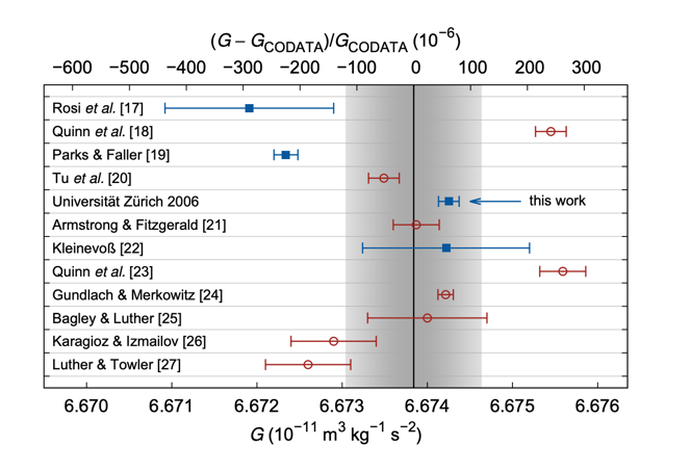
Summary of the History of Measuring G though several ways
CODATA
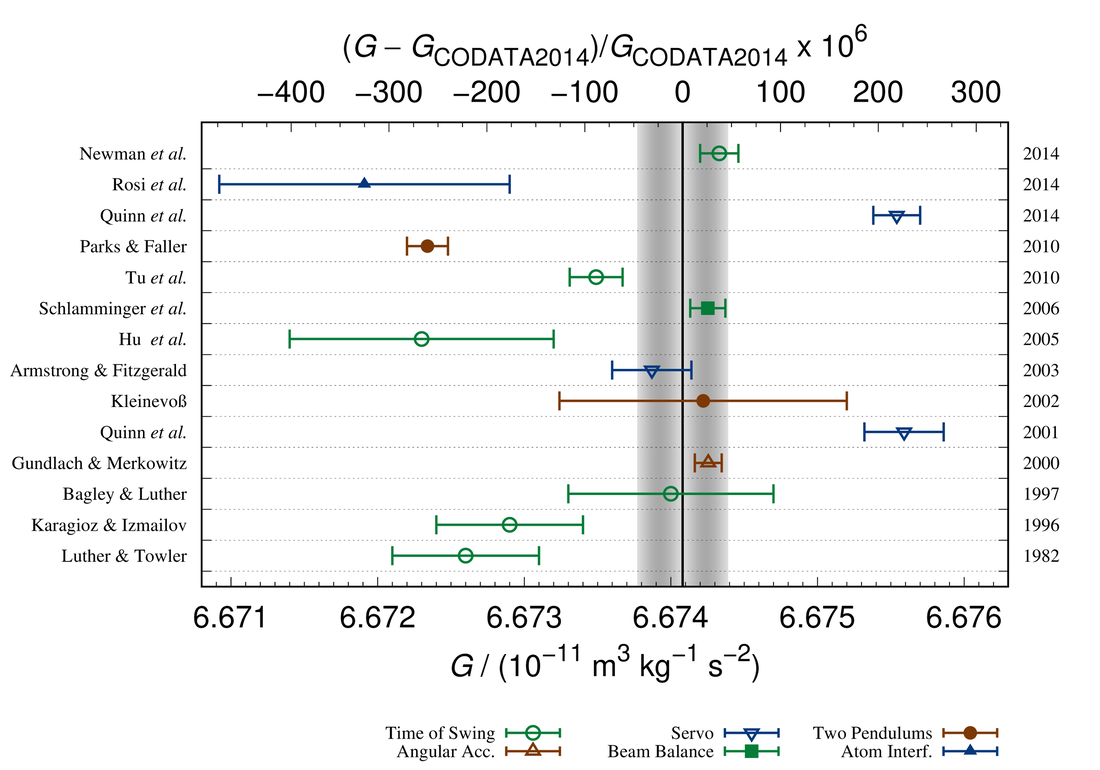
Since then, more than 200 experiments have been performed to determine G. The Committee on Data for Science and Technology published an updated G value (CODATA-2014).
.07% Difference from lowest to highest. 7 parts in 10,000!
Since then, more than 200 experiments have been performed to determine G. The Committee on Data for Science and Technology published an updated G value (CODATA-2014).
.07% Difference from lowest to highest. 7 parts in 10,000!
Peer-reviewed publications measuring the Gravitational Constant

- 4) The BIPM measurements of the Newtonian constant of gravitation, G
- Terry Quinn, Clive Speake, Harold Parks, and Richard Davis
- Published 2014
Flat earthers are always asking for evidence of mass attracting mass, and the best answer for this is the Cavendish experiment which includes now 200-300 peer reviewed studies confirming G to great accuracy. I have personally done this experiment myself, and I actually HAVE a cavendish device!
Careful Cavendish experiments like this measure the strength of the mass to mass attraction, not just THAT it exists but it is a measurement of the exact quantity and magnitude.
Referring to below: A= four source masses, B= test masses, C= whole apparatus rotates, D=dotted lines around boundaries of vacuum chamber to isolate it from air currents. The whole thing is at the same electrostatic potential so the electrostatic forces are negated. It is horizontal and NOT VERTICAL so no electrostatic gradient or voltage argument can hold.
This and similar experiments are real and empirical measurements of mass attracting mass and they explain in painstaking detail how they did it! This experiment is literally a PARAGON of HOW SCIENCE IS DONE! The evidence for gravity existing is overwhelming! - The torsion bar is in a vacuum chamber
- Tested and controlled for magnetic susceptibility Copper-Tellurium alloy masses
- https://royalsocietypublishing.org/doi/full/10.1098/rsta.2014.0032
- https://royalsocietypublishing.org/doi/pdf/10.1098/rsta.2014.0032
- Direct PDF Download
1) Measurement of Newton’s Constant Using a Torsion Balance with Angular Acceleration Feedback
- Jens H. Gundlach, Stephen M. Merkowitz
- Stainless steel non-magnetic masses, gold coated glass plated torsion bar, electrically grounded, torsion bar in 10-5 vacuum
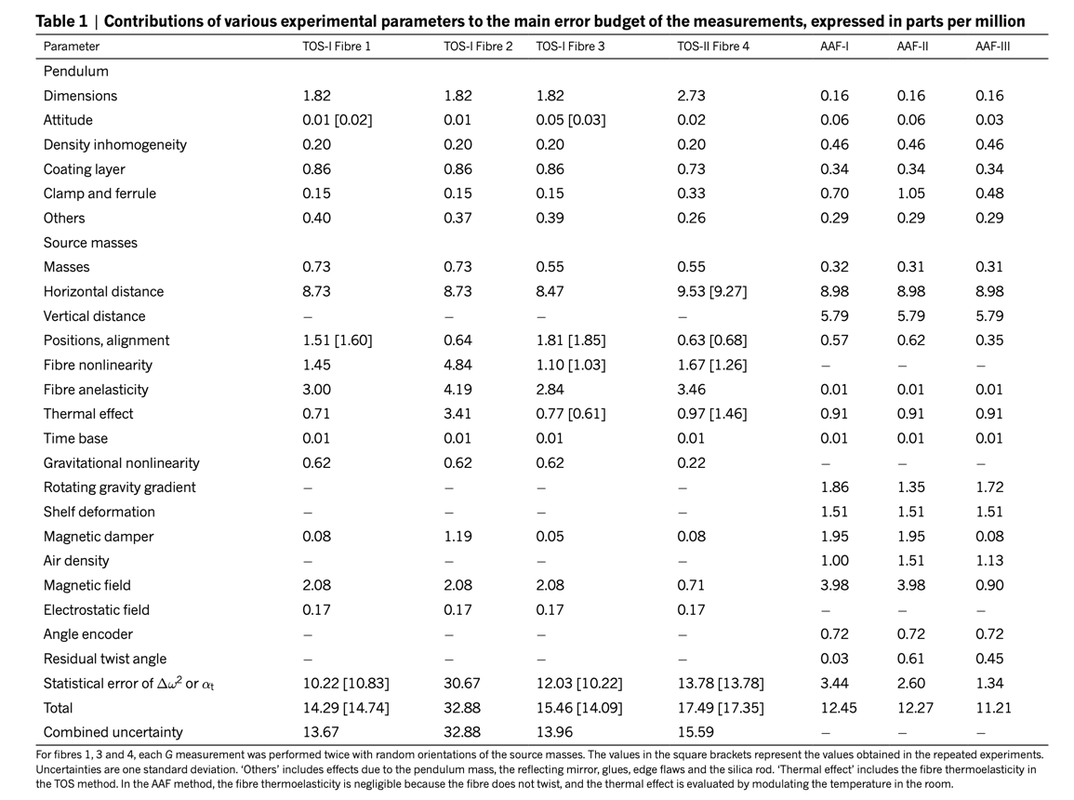
- We measured Newton’s gravitational constant G using a new torsion balance method. Our technique greatly reduces several sources of uncertainty compared to previous measurements: (1) it is insensitive to anelastic torsion fiber properties; (2) a flat plate pendulum minimizes the sensitivity due to the pendulum density distribution; (3) continuous attractor rotation reduces background noise.
- https://arxiv.org/abs/gr-qc/0006043
- Direct PDF Download
- 2) Measurements of the gravitational constant using two independent methods
- Li, Qing & Xue, et al, June 2018
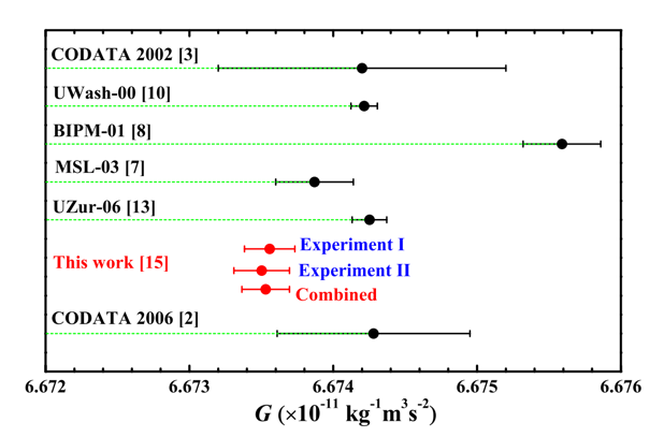
- Here we report two independent determinations of G using torsion pendulum experiments with the time-of-swing method and the angular-accelerationfeedback method. We obtain G values of 6.674184×10−11 and 6.674484×10−11 cubic metres per kilogram per second squared, with relative standard uncertainties of 11.64 and 11.61 parts per million, respectively. These values have the smallest uncertainties reported until now, and both agree with the latest recommended value within two standard deviations.
- https://www.nature.com/articles/s41586-018-0431-5
- Direct PDF download
3) Improved Determination of G Using Two Methods
- Improved Determination of G Using Two Methods
- Terry Quinn, Harold Parks, Clive Speake, and Richard Davis
Phys. Rev. Lett. 111, 101102 – Published 5 September 2013 - https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.111.101102
- Direct PDF Download
- Terry Quinn, Harold Parks, Clive Speake, and Richard Davis
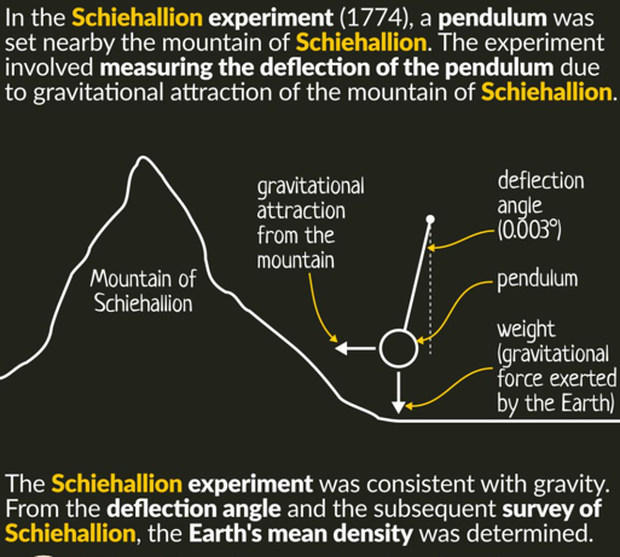
- 5) Mount Schehallion
- The experiment involved measuring the tiny deflection of the vertical due to the gravitational attraction of a nearby mountain. Schiehallion was considered the ideal location after a search for candidate mountains, thanks to its isolation and almost symmetrical shape.
The deflection angle depended on the relative densities and volumes of the Earth and the mountain: if the density and volume of Schiehallion could be ascertained, then so could the density of the Earth. Once this was known, it would in turn yield approximate values for those of the other planets, their moons, and the Sun, previously known only in terms of their relative ratios.
An Account of Observations Made on the Mountain Schiehallion for Finding Its Attraction- Nevil Maskelyne, 1775
- https://royalsocietypublishing.org/doi/10.1098/rstl.1775.0050
- Direct PDF Download
- An Account of the Calculations Made from the Survey and Measures Taken at Schehallien
6) A modern and more accurate look at Mt Schiehallion
A modern re-examination of the geophysical data was able to take account of factors the 1774 team could not. With the benefit of a 120-km radius digital elevation model, greatly improved knowledge of the geology of Schiehallion, and the help of a computer, a 2007 report produced a mean Earth density of 5,480 ± 250 kg·m−3. When compared to the modern figure of 5,515 kg·m−3, it stood as a testament to the accuracy of Maskelyne's astronomical observations.
https://www.lyellcollection.org/doi/10.1144/sjg43010015
Smallwood, J.R. (2007). "Maskelyne's 1774 Schiehallion experiment revisited". Scottish Journal of Geology. 43 (1): 15–31
A modern re-examination of the geophysical data was able to take account of factors the 1774 team could not. With the benefit of a 120-km radius digital elevation model, greatly improved knowledge of the geology of Schiehallion, and the help of a computer, a 2007 report produced a mean Earth density of 5,480 ± 250 kg·m−3. When compared to the modern figure of 5,515 kg·m−3, it stood as a testament to the accuracy of Maskelyne's astronomical observations.
https://www.lyellcollection.org/doi/10.1144/sjg43010015
Smallwood, J.R. (2007). "Maskelyne's 1774 Schiehallion experiment revisited". Scottish Journal of Geology. 43 (1): 15–31
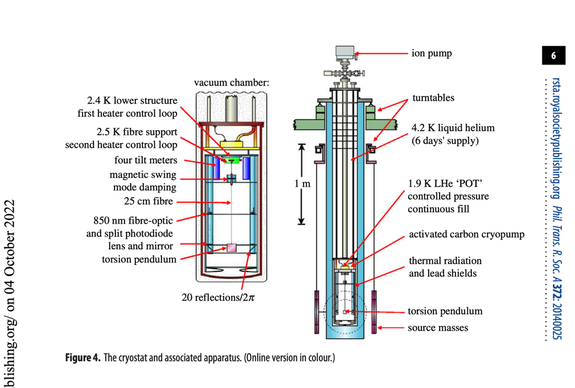
- 7) A measurement of G with a cryogenic torsion pendulum
- Riley Newman1, Michael Bantel1,2, Eric Berg1 and William Cross1 (2014)
- 1Department of Physics, University of California Irvine, Irvine, CA 92697-4575, USA
- Underground bunker, liquid helium, vacuum, 59kg copper masses. A measurement of Newton’s gravitational constant G has been made with a cryogenic torsion pendulum operating below 4 K in a dynamic mode in which G is determined from the change in torsional period when a field source mass is moved between two orientations. The source mass was a pair of copper rings that produced an extremely uniform gravitational field gradient, whereas the pendulum was a thin fused silica plate, a combination that minimized the measurement’s sensitivity to error in pendulum placement.
- https://royalsocietypublishing.org/doi/pdf/10.1098/rsta.2014.0025
- Direct PDF Download
- Riley Newman1, Michael Bantel1,2, Eric Berg1 and William Cross1 (2014)
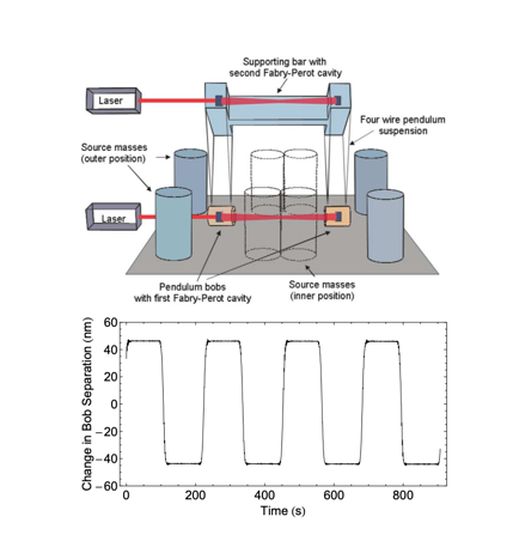
- 8) A Simple Pendulum Determination of the Gravitational Constant
- Harold V. Parks, and James E. Faller (2018)
- We determined the Newtonian Constant of Gravitation G by interferometrically measuring the change in spacing between two free-hanging pendulum masses caused by the gravitational field from large tungsten source masses.
- https://arxiv.org/abs/1008.3203
- https://arxiv.org/pdf/1008.3203.pdf
- Direct PDF Download
- 9) New determination of the gravitational constant G with time-of-swing method
- Inside a vacuum chamber at 10-5 Pa.
- Extremely thorough methodology
- https://www.researchgate.net/publication/255039364_New_determination_of_the_gravitational_constant_G_with_time-of-swing_method
- Direct PDF Download
- 10) Reflections on a Measurement of the Gravitational Constant Using a Beam Balance and 13 Tons of Mercury
- Commentary on “Determination of the Gravitational Constant with a Beam Balance”
- S. Schlamminger, R.E. Pixley, F. Nolting, J. Schurr4 and U. Straumann
- https://arxiv.org/abs/1407.5214
- Direct PDF Download
- 11) Measuring Earth's Curvature!
Determination of the Newtonian Gravitational Constant Using Atom Interferometry- G. Lamporesi, A. Bertoldi, L. Cacciapuoti, M. Prevedelli, and G.M. Tino
- Dated: October 27, 2018
- https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.100.050801
- http://coldatoms.lens.unifi.it/tino/images/personal/articles/magia/lamporesi08.pdf
- Direct PDF Download
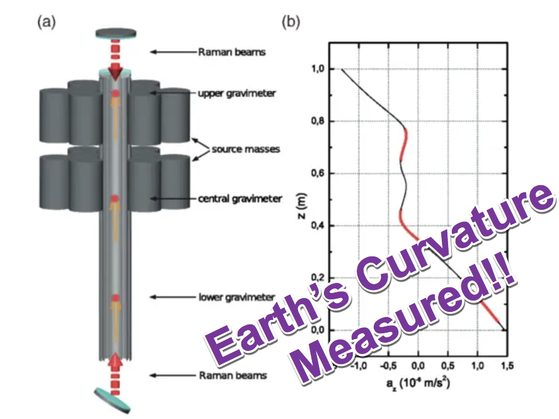
We know with precision that the Earth’s gravitational pull gradually decreases with increasing altitude. Now a team has taken the next step by measuring the change in this gravity gradient produced by a large mass, using measurements at three different heights.
The technique of atom interferometry enables distance measurements with extremely high precision. It has been used previously to measure the strength of gravitational fields and also the rate of change in those fields over some distance (the gradient). Together such measurements permit Newton’s gravitational constant G to be determined. Measuring gravity at two close locations gives the gradient as the difference between the two divided by their separation distance; measuring at three locations gives the rate of change of the gradient, which is also called the curvature of the field.
The technique of atom interferometry enables distance measurements with extremely high precision. It has been used previously to measure the strength of gravitational fields and also the rate of change in those fields over some distance (the gradient). Together such measurements permit Newton’s gravitational constant G to be determined. Measuring gravity at two close locations gives the gradient as the difference between the two divided by their separation distance; measuring at three locations gives the rate of change of the gradient, which is also called the curvature of the field.
- 12) SMALL MASSES! Measurement of gravitational coupling between millimetre-sized masses
- Tobias Westphal, Hans Hepach, Jeremias Pfaff & Markus Aspelmeyer
- 2021-03-10
- Here we show gravitational coupling between two gold spheres of 1 millimetre radius, thereby entering the regime of sub-100-milligram sources of gravity.
- https://doi.org/10.1038/s41586-021-03250-7