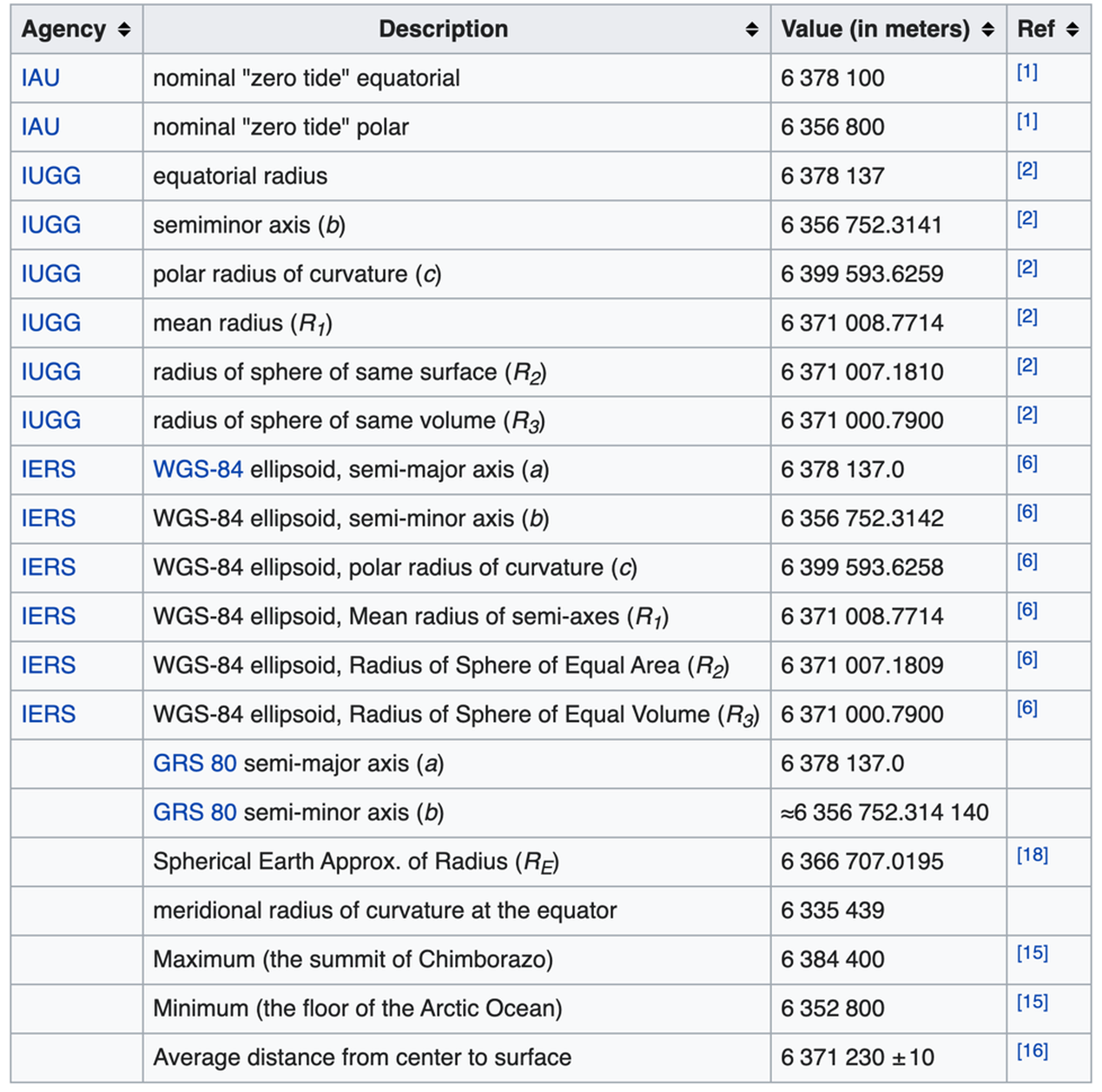
Radius Measurements of the Earth/Curvature Studies
- George Biddel Airy, Esq., A.M, F.R.S., Astronomer Royal
- Originally Published 1830
- Encyclopædia Metropolitana, Volume V, Article: Figure of the Earth
- Pages 185-260
- Specific numbers on Page 240
- a = 20,923,700 feet = 6,377,543.76 meters
- b = 20,853,810 feet = 6,356,241.288 meters
- Direct PDF Download
- Alexander Ross Clarke
- Published 1833
- Account of the Observations and Calculations, of the Principal Triangulation; and of the Figure, Dimensions and Mean Specific Gravity of the Earth as Derived Therefrom
- Survey of Great Britain
- a = 20,927,005 feet = 6,378,551.12 meters
- c = 280.4 feet = 85.47 meters
- https://books.google.com/books?id=DKELAQAAIAAJ
- Direct PDF Download
- Friedrich Wilhelm Bessel
- Published 1841
- Astronomische Nachrichten 333 and 438
- a = 3,272,077.14 toises = 20,922,829.22 feet = 6,377,278.35 meters
- b = 3,261,139.33 toises = 20,852,888.96 feet = 6,355,960.55 meters
- Astronomische Nachrichten 333:
- Astronomische Nachrichten 438
- Sir George Everest
- Published 1847
- Account of the Measurement of Two Sections of the Meridional Arc of India between the Parallels of 18° 3′ and 29° 30′
- a = 20,920,902 feet = 6,376,690.93 meters
- b = 20,853,642 feet = 6,356,190.08 meters
- https://books.google.com/books/about/An_Account_of_the_Measurement_of_Two_Sec.html?id=ne82AQAAMAAJ
- Direct PDF Download
- “Transcontinental Triangulation and the American Arc of the Parallel”
- Published 1900
- Ocean to ocean survey. Shows triangulation with spherical excess.
- Page 221 for Spherical Excess
- From page 901 of the PDF, number 3 in the list is the primary result of this survey.
- a = 6,377,912 meters
- b = 6,356,309 meters
- https://geodesy.noaa.gov/library/pdfs/Special_Publication_No_4.pdf
- Direct PDF Download: Transcontinental Triangulation and the American Arc of the Parallel
- “The Figure of the Earth and Isostasy from Measurements in the United States”
- Published 1909
- Used the results from several surveys to determine the equatorial and polar radius of the earth.
- Page 174 has the conclusions of the computations.
- a = 6,378,283±34 meters
- b = 6,356,868 meters
- https://hdl.handle.net/2027/hvd.hnwwbh
- Direct PDF Download
Eratosthenes Experiment - First Calculation of R.
In 205 BC, Eratosthenes successfully determined the circumference of the Earth by measuring the length of the shadow cast by a rod. He did the measurement in Alexandria and timed it to coincidence when the Sun is directly overhead Syene.
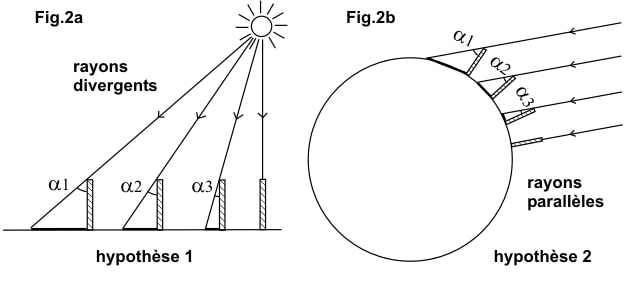
Eratosthenes did his experiment by taking measurements in two locations: Alexandria and Syene. But we can easily modify his experiment by making measurements in three or more places, and the flat-Earth model is instantly proven wrong.
Using the flat-Earth model, the length of the shadow will have a linear response. On the other hand, using the spherical Earth model, the length of the shadow has a non-linear response. We can also observe that in near-polar locations, the experiment will result in a very long shadow. The flat-Earth model cannot explain this phenomenon.
Furthermore, the flat-Earth model will not produce a consistent result. It is not a coincidence that not a single flat-Earther can give us the exact distance to the Sun. Their outcome will vary a lot even though this experiment does not demand high precision and accuracy.
From this fact, we can easily conclude the Earth is spherical, not flat.
You can do the calculation yourself without any traveling by using the data provided by Eratosthenes.eu. This website attempts to pair two schools from around the world and help them redo the Eratosthenes experiment as a teaching aid. Their data is publicly available and can be used for our purpose.
In 205 BC, Eratosthenes successfully determined the circumference of the Earth by measuring the length of the shadow cast by a rod. He did the measurement in Alexandria and timed it to coincidence when the Sun is directly overhead Syene.
Eratosthenes did his experiment by taking measurements in two locations: Alexandria and Syene. But we can easily modify his experiment by making measurements in three or more places, and the flat-Earth model is instantly proven wrong.
Using the flat-Earth model, the length of the shadow will have a linear response. On the other hand, using the spherical Earth model, the length of the shadow has a non-linear response. We can also observe that in near-polar locations, the experiment will result in a very long shadow. The flat-Earth model cannot explain this phenomenon.
Furthermore, the flat-Earth model will not produce a consistent result. It is not a coincidence that not a single flat-Earther can give us the exact distance to the Sun. Their outcome will vary a lot even though this experiment does not demand high precision and accuracy.
From this fact, we can easily conclude the Earth is spherical, not flat.
You can do the calculation yourself without any traveling by using the data provided by Eratosthenes.eu. This website attempts to pair two schools from around the world and help them redo the Eratosthenes experiment as a teaching aid. Their data is publicly available and can be used for our purpose.
Only One Point Needed to Calculate R
Al Bee-rooni
Al-Biruni was one of the great medieval scholars, well versed in physics, mathematics, astronomy, and natural sciences. He spent a large part of his life in Afghanistan. He is regarded as the father of geodesy for his important contributions to that field.
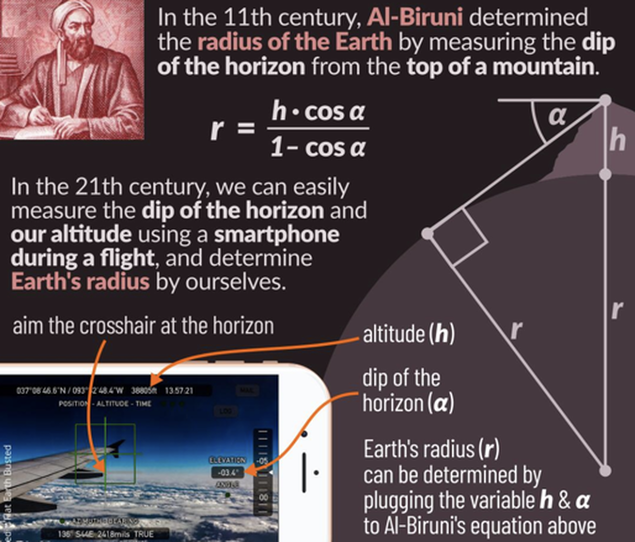
Abu Rayhan al-Biruni accurately determined the Earth radius by formulating a trigonometric equation relating the dip angle (between the true horizon and astronomical horizon) observed from the top of a mountain to the height of that mountain.
Al Bee-rooni
Al-Biruni was one of the great medieval scholars, well versed in physics, mathematics, astronomy, and natural sciences. He spent a large part of his life in Afghanistan. He is regarded as the father of geodesy for his important contributions to that field.
Abu Rayhan al-Biruni accurately determined the Earth radius by formulating a trigonometric equation relating the dip angle (between the true horizon and astronomical horizon) observed from the top of a mountain to the height of that mountain.
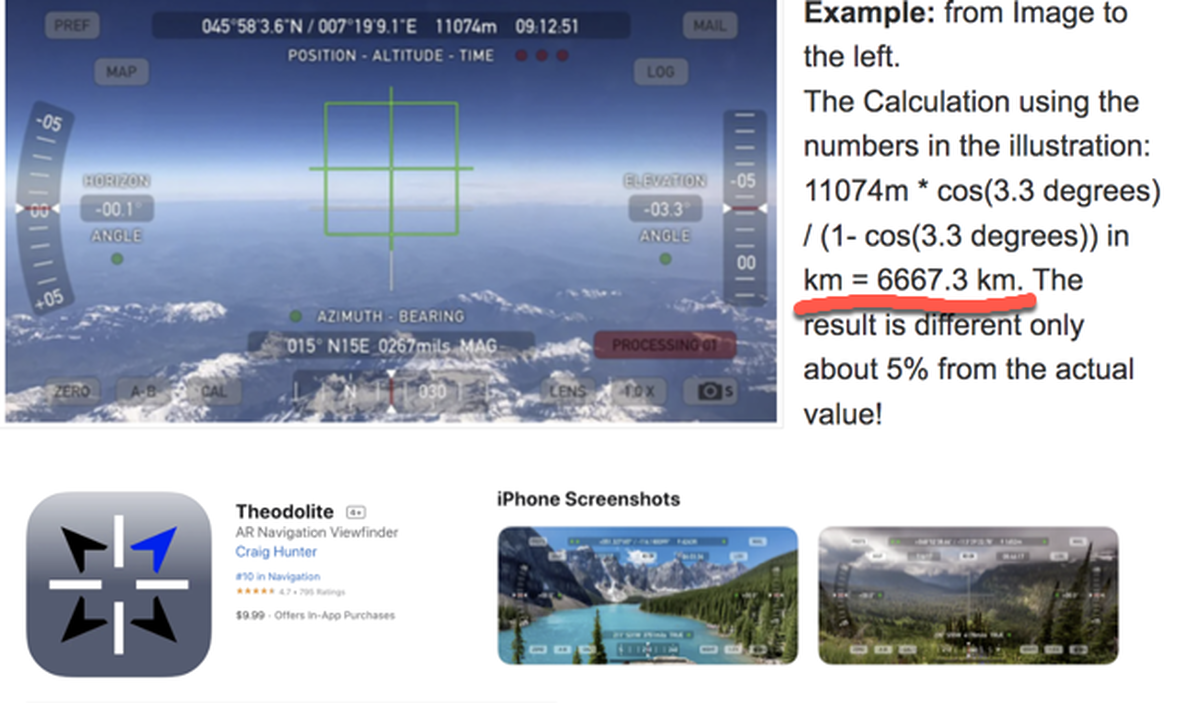
Calculating the Radius of the Earth with a Theodolite
You can download the Theodolite app on your iPhone which uses the accelerometers to position a reticle in the camera view marking out level & plumb and has indicators showing the angle of the camera in relationship to level. If you are at high altitude like an airplane this will help to make the results more accurate. You can calculate the radius of the earth with some decent accuracy doing this.
Also notice from these images, you DO have to look down to see the horizon -- exactly as much as expected on a Globe of 3959 miles radius and we can observe the Dip angle increasing exactly as expected:
You can download the Theodolite app on your iPhone which uses the accelerometers to position a reticle in the camera view marking out level & plumb and has indicators showing the angle of the camera in relationship to level. If you are at high altitude like an airplane this will help to make the results more accurate. You can calculate the radius of the earth with some decent accuracy doing this.
Also notice from these images, you DO have to look down to see the horizon -- exactly as much as expected on a Globe of 3959 miles radius and we can observe the Dip angle increasing exactly as expected:

1. Assume earth is spherical
2. Horizon up to star
Bottom up matching the globe math.
Measurements by professional surveyors.
Network of triangles they create
Showing the measurement of curvature.
Level is a curved surface.
Spherical excess.
Surface of a convex structure of some source.
Each one of those those triangles you can get radius of earth.
2. Horizon up to star
Bottom up matching the globe math.
Measurements by professional surveyors.
Network of triangles they create
Showing the measurement of curvature.
Level is a curved surface.
Spherical excess.
Surface of a convex structure of some source.
Each one of those those triangles you can get radius of earth.