"No one must think that Newton’s great creation can be overthrown in any real sense by this or by any other theory. His clear and wide ideas will forever retain their significance as the foundation on which our modern conceptions of physics have been built."
-Albert Einstein
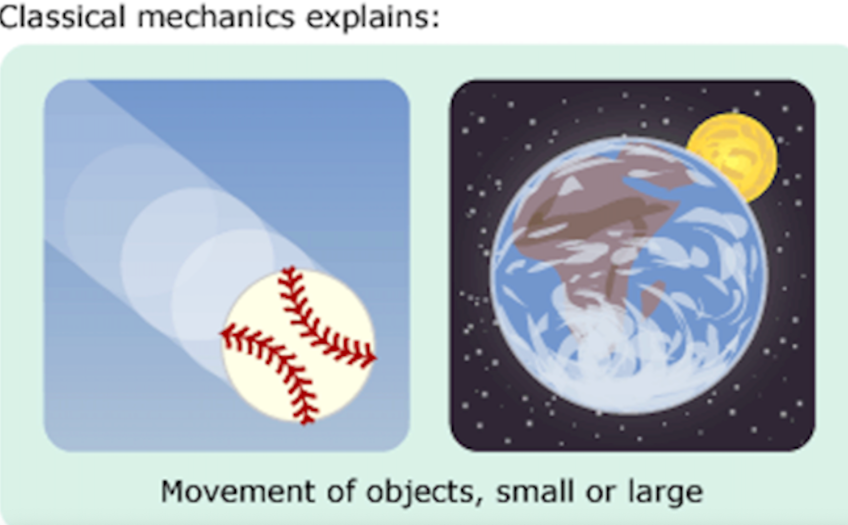
Four main areas of science that cover the Universe
1. Newtons Laws for our Inertial reference frame
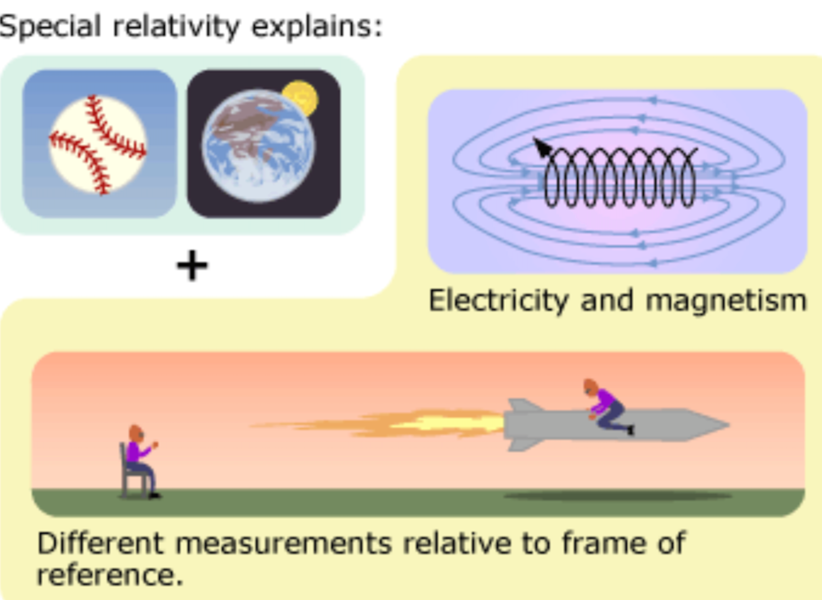
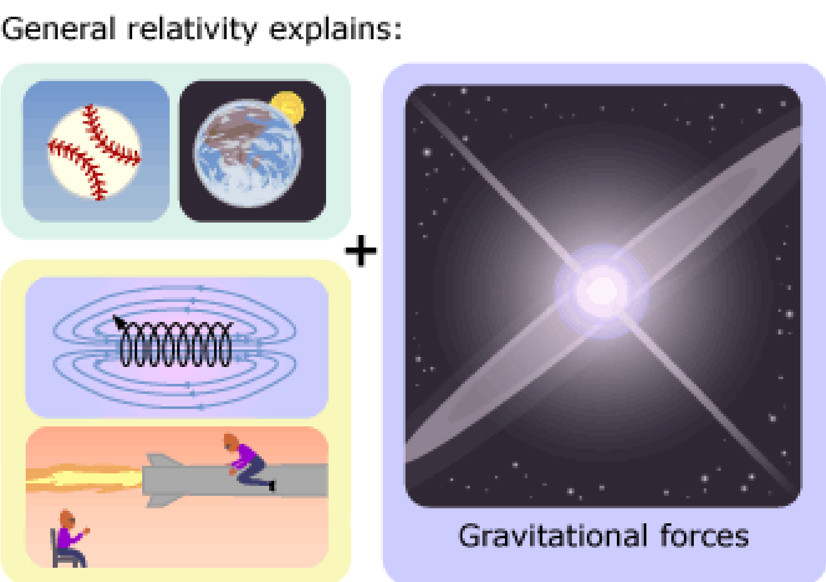
2. General Relativity - Better
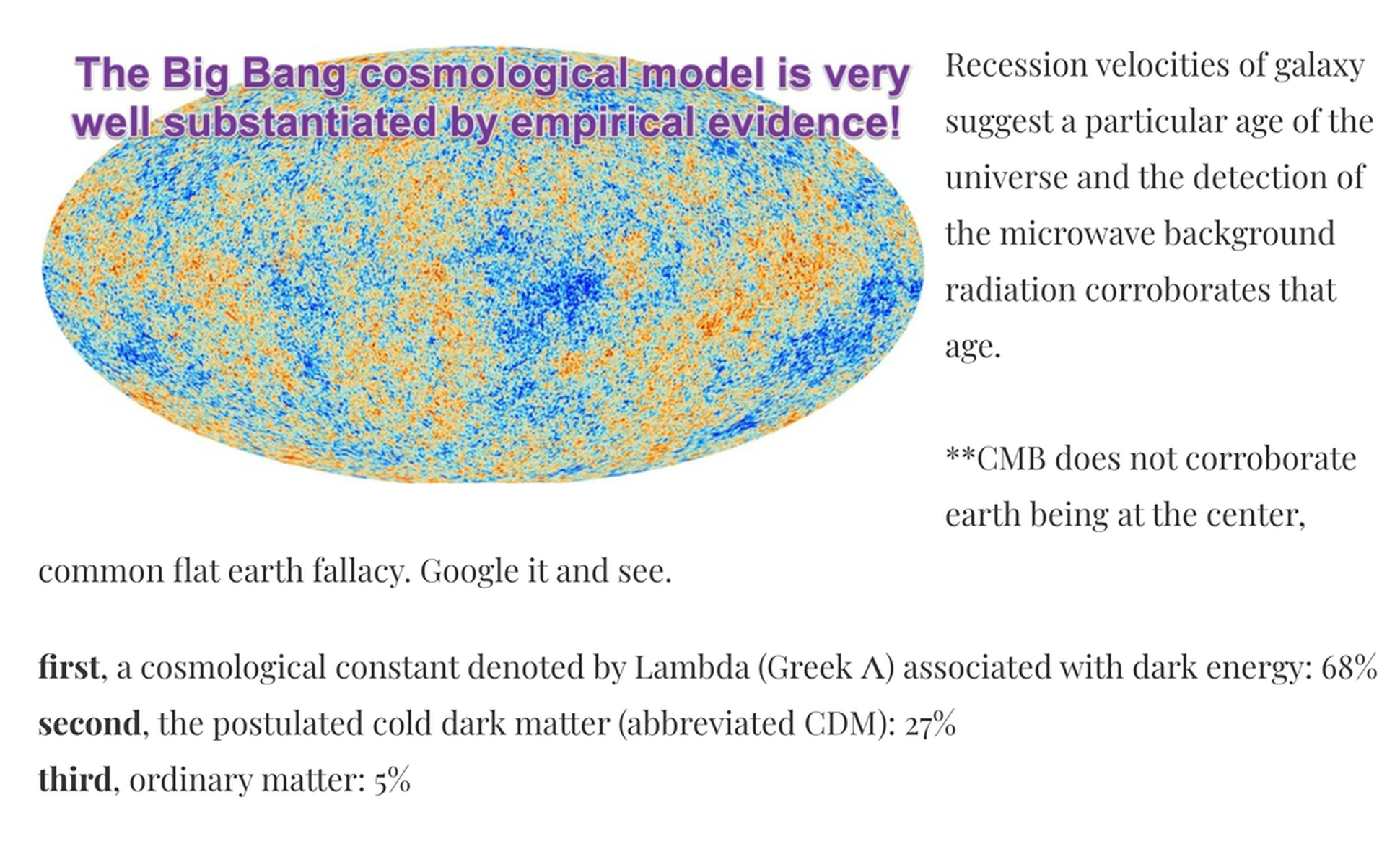
3. Big Bang cosmological model
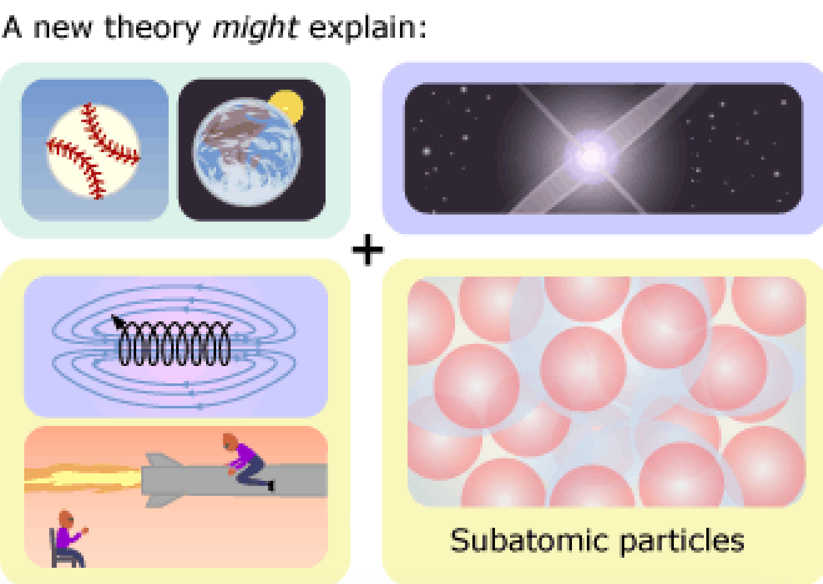
4. Quantum Mechanics
Flat Earth Objections
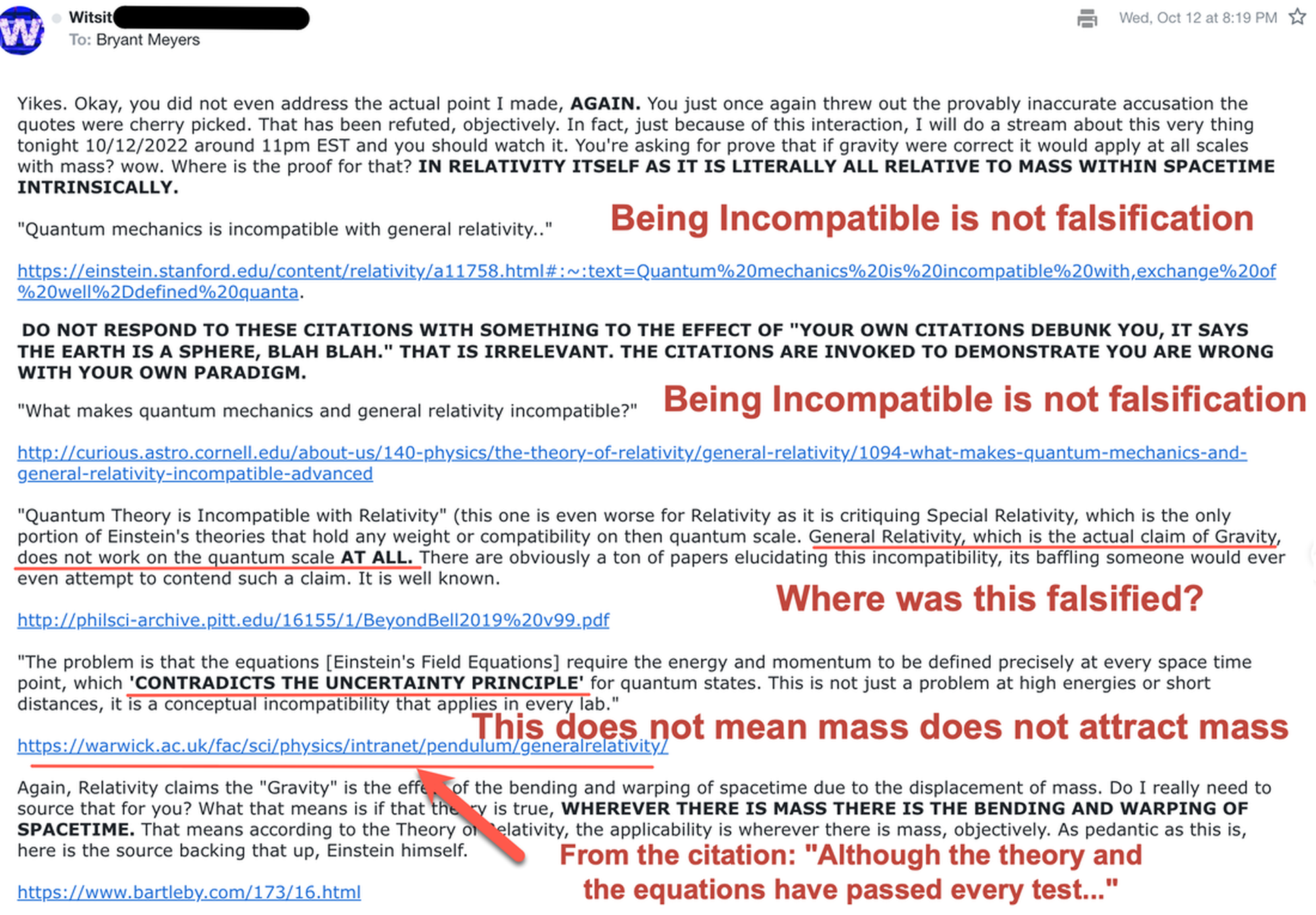
QM incompatible with GR
95% mass/energy in the universe is not understood
Dark Matter
Dark Energy
120 degrees of magnitude mistmatch
-Albert Einstein
Four main areas of science that cover the Universe
1. Newtons Laws for our Inertial reference frame
2. General Relativity - Better
3. Big Bang cosmological model
4. Quantum Mechanics
Flat Earth Objections
QM incompatible with GR
95% mass/energy in the universe is not understood
Dark Matter
Dark Energy
120 degrees of magnitude mistmatch
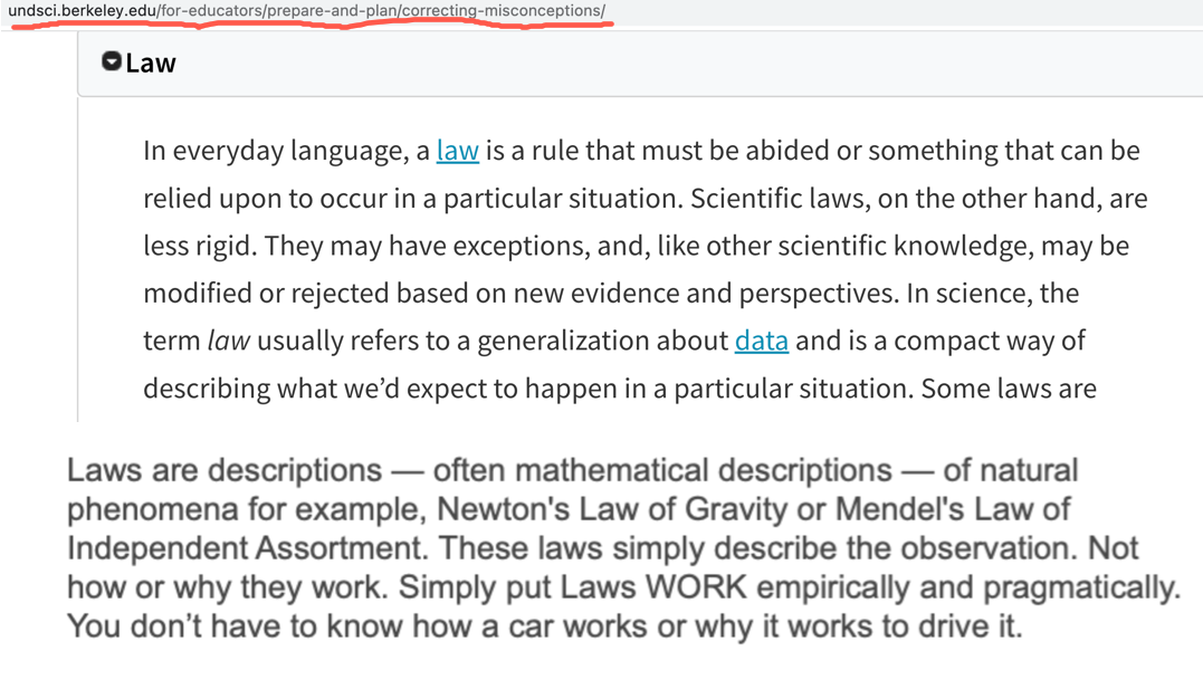
Newtons Universal Law of Gravitation and Einsteins General Relativity as LAWS of Science.
Newtons Laws for EXCELLENT in our Barycentric/heliocentric Solar System! The margin of error is miniscule and only really impacts Mercury because it is a SMALL planet that is closest to our Massive sun. Perihellion is a common cosmological even of massive enough and/or close enough orbiting bodies. Correction term in GR predicts this to MANY decimal places.
Scientific Laws and Margin of Error for making predictions
Newtons Laws Work EXCELLENT in their domain large size/mass, slow speeds, weak gravity, barycentric inertial frame (no dark matter influence).
Quantum Mechanics - Matter waves , high mass and long regeneration time
Relativity - Slow speeds and flat space
Dark Matter Energy - Subtle influence on Cosmic scale. (1.5 meters in billions of miles).
Laws of Science WORK! They don't say or even claim to say WHY they work, but they do through repeated observation, testing, experiments and most importantly applications in engineering to MAKE ACTUAL THINGS THAT WORK!! You cannot engineer things that work in the world if the law or science behind it is wrong!
Newtons Laws for EXCELLENT in our Barycentric/heliocentric Solar System! The margin of error is miniscule and only really impacts Mercury because it is a SMALL planet that is closest to our Massive sun. Perihellion is a common cosmological even of massive enough and/or close enough orbiting bodies. Correction term in GR predicts this to MANY decimal places.
Scientific Laws and Margin of Error for making predictions
Newtons Laws Work EXCELLENT in their domain large size/mass, slow speeds, weak gravity, barycentric inertial frame (no dark matter influence).
Quantum Mechanics - Matter waves , high mass and long regeneration time
Relativity - Slow speeds and flat space
Dark Matter Energy - Subtle influence on Cosmic scale. (1.5 meters in billions of miles).
Laws of Science WORK! They don't say or even claim to say WHY they work, but they do through repeated observation, testing, experiments and most importantly applications in engineering to MAKE ACTUAL THINGS THAT WORK!! You cannot engineer things that work in the world if the law or science behind it is wrong!
We use Scientific laws to make accurate predictions about the Inertial Earth/Sun Solar System System we live in.
They are not perfect, they are not "proven" but they have OVERWHELMING evidence to support them and have never been falsified within their domain of applicability and parameters. The FACT they are used in engineering to make things that are all around us is great testament to their validity!!
They are not perfect, they are not "proven" but they have OVERWHELMING evidence to support them and have never been falsified within their domain of applicability and parameters. The FACT they are used in engineering to make things that are all around us is great testament to their validity!!
Just because Newton didn't know the mechanism doesn't mean Newton Laws are not a law. The definition of a scientific law doesn't state the inventor of the law needs to know the mechanism?? They work in our inertial reference frame!
===> Einstein gave a better answer for the mechanism and likely a quantum theory of gravity better yet.
Just because Mendel didn't know why hereditary traits were passed on doesn't make Mendels law any less valid. They Work!
===> Darwin gave a better understanding for laws of hereditary and likely a better theory of evolution will come along
Just because Snell didn't know the mechanism behind Snell's laws doesn't make any difference. THEY WORK.
===> Quantum mechanics gave a better understanding of Snell's laws
===> Einstein gave a better answer for the mechanism and likely a quantum theory of gravity better yet.
Just because Mendel didn't know why hereditary traits were passed on doesn't make Mendels law any less valid. They Work!
===> Darwin gave a better understanding for laws of hereditary and likely a better theory of evolution will come along
Just because Snell didn't know the mechanism behind Snell's laws doesn't make any difference. THEY WORK.
===> Quantum mechanics gave a better understanding of Snell's laws
1. Newtons Laws
We have overwhelming evidence that mass attracts mass.
We have overwhelming evidence that mass attracts mass.
- G is a constant. If you understand science, you would know about the inherent problems of taking measurements.
Getting a measurement of G is a delicate process. Done for the first tome in 1978 6.64x10E-11
Discrepancies out to 5 or 6 decimals, SO IT IS A CONSTANT!
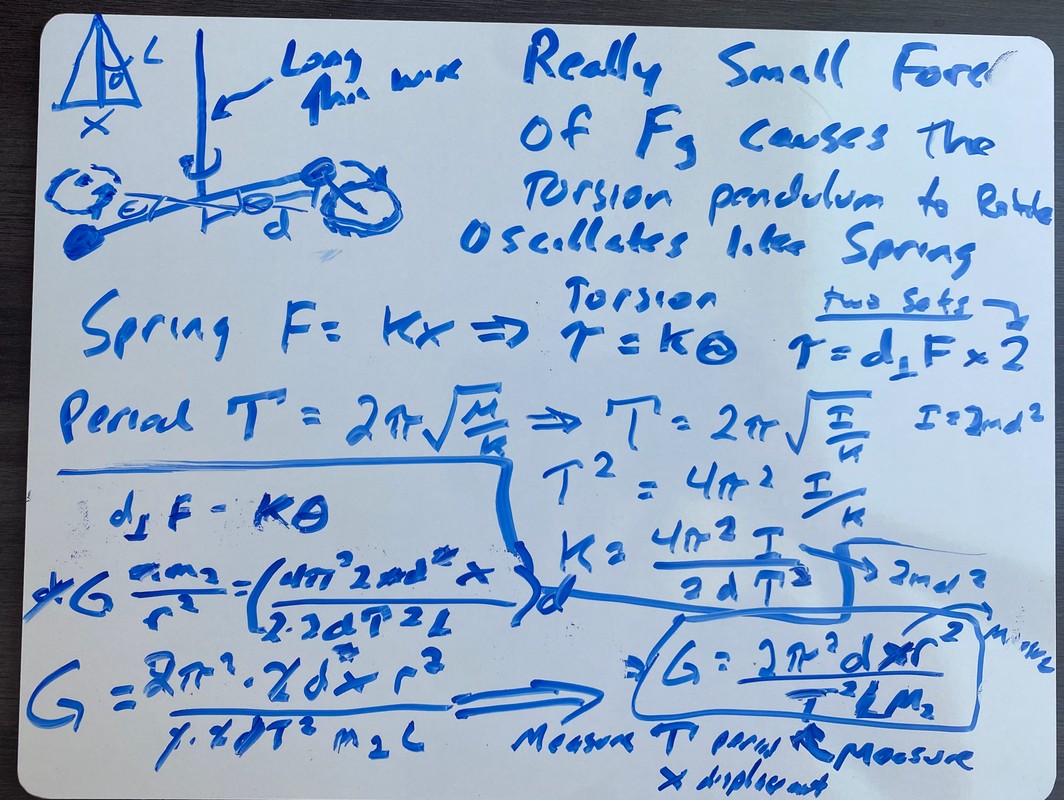
I have a Cavendish device and have done the experiment as have thousands of students every year and hundreds and hundreds of labs have done with amazing precision. When done carefully, it very accurately measures the gravitational constant which you can then use to accurately measure the mass of the earth and CONFIRM the downward acceleration (The Flat earth has NO model and hence no way to predict this downward acceleration which we all observe). Also these accurate calculations allow us to use Newton's laws with AMAZING accuracy! Success leaves clues and Literally the world around you (all the buildings, bridges, roads, structures, etc are ALL based on Newton's laws).
The most sensitive Cavendish ever performed confirms G, the gravitational constant to 5 decimal places.
This is EMPIRICAL PROOF of Newton's Universal Law of gravity and proof Newtons laws work. Newton's Universal Law of Gravitation is a Law because it always works and NEVER has been disproven in its domain of application (speeds not near the speed of light and gravitational fields not too extreme). Never falsified. On earth they work perfectly, because we don't live on a black hole, and we are not traveling near the speed of light. If we were in these extreme conditions we would need to use General Relativity which is more accurate but extremely difficult to work with.
The most sensitive Cavendish ever performed confirms G, the gravitational constant to 5 decimal places.
This is EMPIRICAL PROOF of Newton's Universal Law of gravity and proof Newtons laws work. Newton's Universal Law of Gravitation is a Law because it always works and NEVER has been disproven in its domain of application (speeds not near the speed of light and gravitational fields not too extreme). Never falsified. On earth they work perfectly, because we don't live on a black hole, and we are not traveling near the speed of light. If we were in these extreme conditions we would need to use General Relativity which is more accurate but extremely difficult to work with.
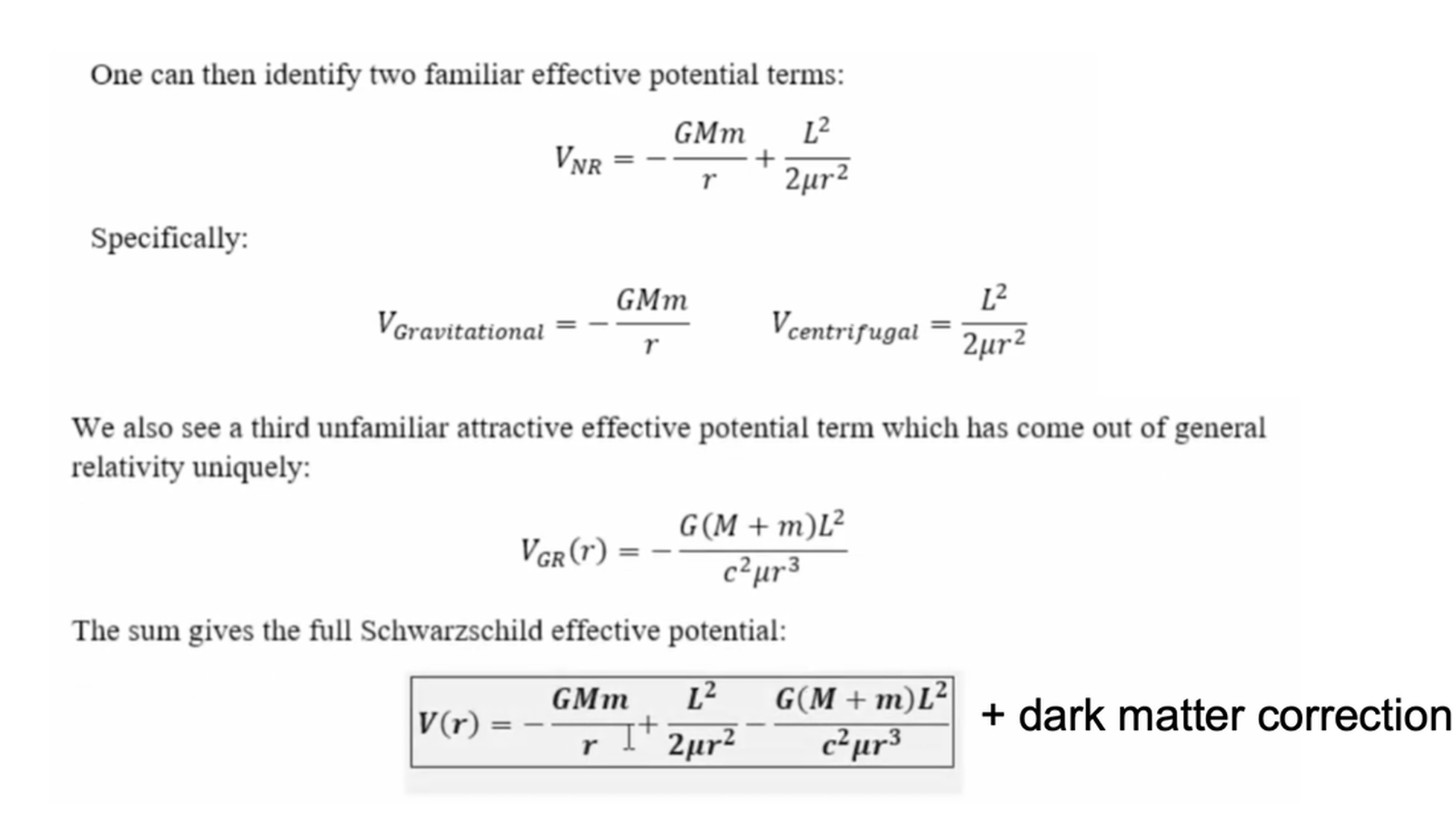
2. General Relativity - Cause of Gravity , the why and how
**General relativity is one of the most corroborated theories in the history of science.
1. Perihelion precession of Mercury
2. Gravitational Lensing (one of first proofs in 1919 during eclipse
3. Black Holes
4. Pound Rebka Experiment
5. LIGO observations - Confirmed Einstein to several decimal places
6. Atom Interferometer
6. GPS - 38uSecond error is not accounted for = 45 (gravity slower) -7 (velocity faster) = 38uS ==> 11km Error!!
**General relativity is one of the most corroborated theories in the history of science.
1. Perihelion precession of Mercury
2. Gravitational Lensing (one of first proofs in 1919 during eclipse
3. Black Holes
4. Pound Rebka Experiment
5. LIGO observations - Confirmed Einstein to several decimal places
6. Atom Interferometer
6. GPS - 38uSecond error is not accounted for = 45 (gravity slower) -7 (velocity faster) = 38uS ==> 11km Error!!
Dark matter is there. Dark matter is not a prediction of a theory that could be proven wrong but an observation. There is more gravitational effect than our models account for. Dark matter is just a placeholder for something we cannot put our finger on at the moment. It has gravitational effect, the only thing we know that has gravitational effect is matter, so we call it matter. And we cannot see it so we call it dark. That’s all there is to it. It might be some entity our models don’t include yet or it might simply be a tiny flaw in our models. But the effect is there. It ensure that Einstein’s theory works on all scales, with no modification.
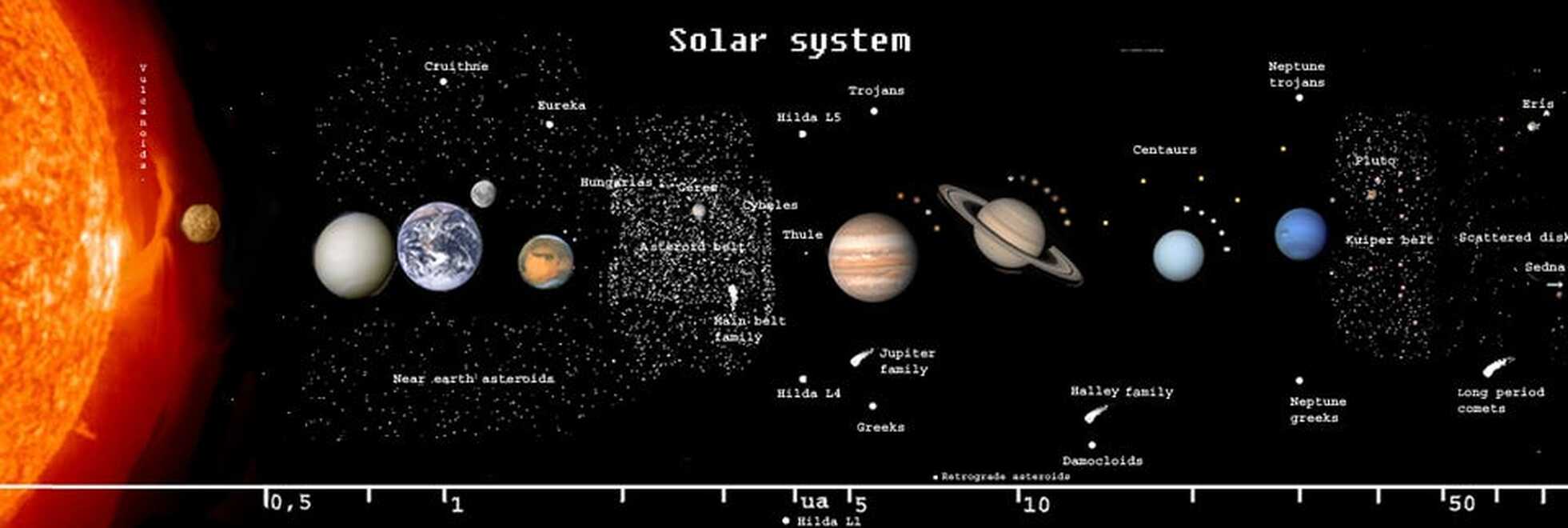
Dark Matter in the Solar System.
Spoiler Alert: It doesn't invalidate Newton or Einstein.
Einstein’s theory works just fine, e.g., on the scale of the solar system
The big question you need to ask is this: compared to the masses of the Sun, the planets, and the other objects in our Solar System, what is the relevant, interesting mass due to dark matter?
Spoiler Alert: It doesn't invalidate Newton or Einstein.
Einstein’s theory works just fine, e.g., on the scale of the solar system
The big question you need to ask is this: compared to the masses of the Sun, the planets, and the other objects in our Solar System, what is the relevant, interesting mass due to dark matter?
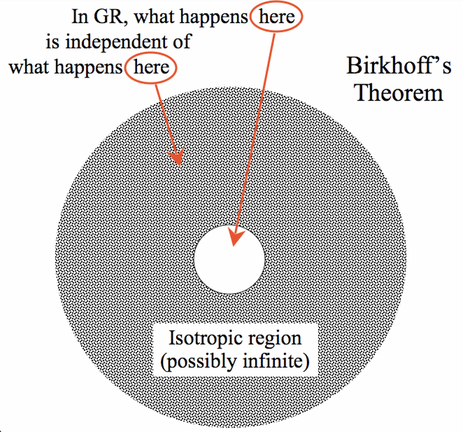
Sun is, by far, the dominant mass in the Solar System. To an outstanding approximation, it determines the orbits of the planets. But for Venus, the planet Mercury is interior to it; to a first approximation, Venus’ orbit is determined by the combined masses of the Sun plus Mercury. For Jupiter, its orbit is determined by the Sun plus the inner, rocky planets and the asteroid belt. And for any orbiting object in general, its orbit is determined by the total mass enclosed by an imaginary sphere centered on the Sun, with that object at the edge of the sphere.
If there’s a sea of dark matter that permeates space where we are — all through the Solar System — the outer planets should see a slightly different (greater) mass than the inner planets. And if there’s enough dark matter, it should be detectable. Because we know the mass of the Milky Way, the relative densities of normal and dark matter, and we have simulations that tell us how the dark matter density ought to behave, we can come up with some very good estimates. When you do these calculations, you find that about 10^13 kg of dark matter ought to be felt by Earth’s orbit, while around 10^17 kg would be felt by a planet like Neptune.
But these values are tiny compared to the other masses of consequence! The Sun has a mass of 2 × 10^30 kg, while Earth is more like 6 × 10^24 kg. Values like the one we came up with, in the 10^13 – 10^17 kg range, are the mass of a single modest asteroid. Someday, we may understand the Solar System well enough that such tiny differences will be detectable, but we’re a good factor of 100,000+ away from that right now.
https://www.forbes.com/sites/startswithabang/2018/03/24/ask-ethan-if-dark-matter-is-everywhere-why-havent-we-detected-it-in-our-solar-system
If there’s a sea of dark matter that permeates space where we are — all through the Solar System — the outer planets should see a slightly different (greater) mass than the inner planets. And if there’s enough dark matter, it should be detectable. Because we know the mass of the Milky Way, the relative densities of normal and dark matter, and we have simulations that tell us how the dark matter density ought to behave, we can come up with some very good estimates. When you do these calculations, you find that about 10^13 kg of dark matter ought to be felt by Earth’s orbit, while around 10^17 kg would be felt by a planet like Neptune.
But these values are tiny compared to the other masses of consequence! The Sun has a mass of 2 × 10^30 kg, while Earth is more like 6 × 10^24 kg. Values like the one we came up with, in the 10^13 – 10^17 kg range, are the mass of a single modest asteroid. Someday, we may understand the Solar System well enough that such tiny differences will be detectable, but we’re a good factor of 100,000+ away from that right now.
https://www.forbes.com/sites/startswithabang/2018/03/24/ask-ethan-if-dark-matter-is-everywhere-why-havent-we-detected-it-in-our-solar-system
Vacuum Catastrophe and Zero Point Energy Casimir Effect
We think that nonrelativistic (Newtonian) mechanics is correct, even though Einstein proved it wrong. Yet we use Newtonian mechanics every day, in a variety of disciplines including engineering and architecture, and we do so successfully.
==> Bill Unruh and collaborators have argued that when the energy density of the quantum vacuum is modeled more accurately as a fluctuating quantum field, the cosmological constant problem does not arise.
Wang, Qingdi; Zhu, Zhen; Unruh, William G. (2017). "How the huge energy of quantum vacuum gravitates to drive the slow accelerating expansion of the Universe". Physical Review D. 95 (10): 103504
==>Another argument, due to Stanley Brodsky and Robert Shrock, is that in light front quantization, the quantum field theory vacuum becomes essentially trivial. In the absence of vacuum expectation values, there is no contribution from QED, weak interactions and QCD to the cosmological constant. It is thus predicted to be zero in a flat space-time
The Cutting Edge
At the farest reaches of our understanding, at the very forefront of science, there are always going to be questions, there will always be things we don't know. Not knowing these things doesn't mean the other stuff they rest upon is wrong.
If there is no dark matter, the earth is still a sphere
The stuff that we don't understand about the galactic rotation, doesn't change the shape of the earth.
In order to quote the dark matter stuff
1. The earth is a globe
2. It's rotating
3. Its orbiting the sun
4. The sun is orbiting the galactic center
5. There are other galaxies very far away
6. We notice they rotate different then we predicted
Just because they rotate slightly differently than predicted, doesn't mean steps 1-5 didn't happen.
At the farest reaches of our understanding, at the very forefront of science, there are always going to be questions, there will always be things we don't know. Not knowing these things doesn't mean the other stuff they rest upon is wrong.
If there is no dark matter, the earth is still a sphere
The stuff that we don't understand about the galactic rotation, doesn't change the shape of the earth.
In order to quote the dark matter stuff
1. The earth is a globe
2. It's rotating
3. Its orbiting the sun
4. The sun is orbiting the galactic center
5. There are other galaxies very far away
6. We notice they rotate different then we predicted
Just because they rotate slightly differently than predicted, doesn't mean steps 1-5 didn't happen.
Problems with Newtonian Gravity and General Relativity and why its not a problem
We think classical mechanics is correct, even though both General Relativity and Quantum Mechanics proved it wrong. Yet we use classical mechanics every day, in a variety of disciplines including engineering and architecture, and we do so successfully: Our machines work, our buildings stand.
Why? Because the old theories were not proven blatantly wrong. What was demonstrated are the limits of their applicability. In everyday scenarios involving nonrelativistic speeds and gravitational fields that are not akin to black holes, Newtonian mechanics gives accurate answers; there’s no need to account for post-Newtonian corrections. In everyday scenarios that do not involve individual atoms or elementary particles (or fast speeds and strong gravity), classical physics works just fine. There’s no need to apply quantum corrections. There is no need to use General Relativity. It would be a waste of effort: a lot of extra computation would be spent on correcting what, a result past the tenth decimal digit?
That doesn’t mean that we don’t know what we are doing. It means we understand exactly how good (or how bad) these theories are, which means we know exactly what we are doing even if we do not have all the answers at cosmic or microscopic scales.
General relativity and quantum field theory yield accurate answers. Very accurate answers, tested through numerous high-precision experiments. Our theoretical works suggests (though by no means proves) that there are limits to their applicability, and that there are probably even better theories out there.
Disproving General Relativity - Dark Matter and Dark Energy
But no, not because of the cosmological constant problem. That has many possible solutions well within the context of quantum field theory, the problem is that in the absence of experimental evidence, we have no basis to pick one over the other, and none of the solutions we know is without issues. There are more fundamental problems: the lack of a quantum theory of gravitation, a satisfactory model for neutrino masses, the ultra high energy behavior of the Standard Model… So no, we do not believe that these theories are the gospel. But as always, physics builds upon existing knowledge. Just as general relativity and quantum physics didn’t invalidate classical mechanics, but rather, refined it and extended its applicability, we expect future theories to also be incremental: existing theories (validated through numerous experiments) will not be discarded, but we will better understand their limits, and we’ll have better theories to probe Nature beyond those limits.
We think classical mechanics is correct, even though both General Relativity and Quantum Mechanics proved it wrong. Yet we use classical mechanics every day, in a variety of disciplines including engineering and architecture, and we do so successfully: Our machines work, our buildings stand.
Why? Because the old theories were not proven blatantly wrong. What was demonstrated are the limits of their applicability. In everyday scenarios involving nonrelativistic speeds and gravitational fields that are not akin to black holes, Newtonian mechanics gives accurate answers; there’s no need to account for post-Newtonian corrections. In everyday scenarios that do not involve individual atoms or elementary particles (or fast speeds and strong gravity), classical physics works just fine. There’s no need to apply quantum corrections. There is no need to use General Relativity. It would be a waste of effort: a lot of extra computation would be spent on correcting what, a result past the tenth decimal digit?
That doesn’t mean that we don’t know what we are doing. It means we understand exactly how good (or how bad) these theories are, which means we know exactly what we are doing even if we do not have all the answers at cosmic or microscopic scales.
General relativity and quantum field theory yield accurate answers. Very accurate answers, tested through numerous high-precision experiments. Our theoretical works suggests (though by no means proves) that there are limits to their applicability, and that there are probably even better theories out there.
Disproving General Relativity - Dark Matter and Dark Energy
But no, not because of the cosmological constant problem. That has many possible solutions well within the context of quantum field theory, the problem is that in the absence of experimental evidence, we have no basis to pick one over the other, and none of the solutions we know is without issues. There are more fundamental problems: the lack of a quantum theory of gravitation, a satisfactory model for neutrino masses, the ultra high energy behavior of the Standard Model… So no, we do not believe that these theories are the gospel. But as always, physics builds upon existing knowledge. Just as general relativity and quantum physics didn’t invalidate classical mechanics, but rather, refined it and extended its applicability, we expect future theories to also be incremental: existing theories (validated through numerous experiments) will not be discarded, but we will better understand their limits, and we’ll have better theories to probe Nature beyond those limits.
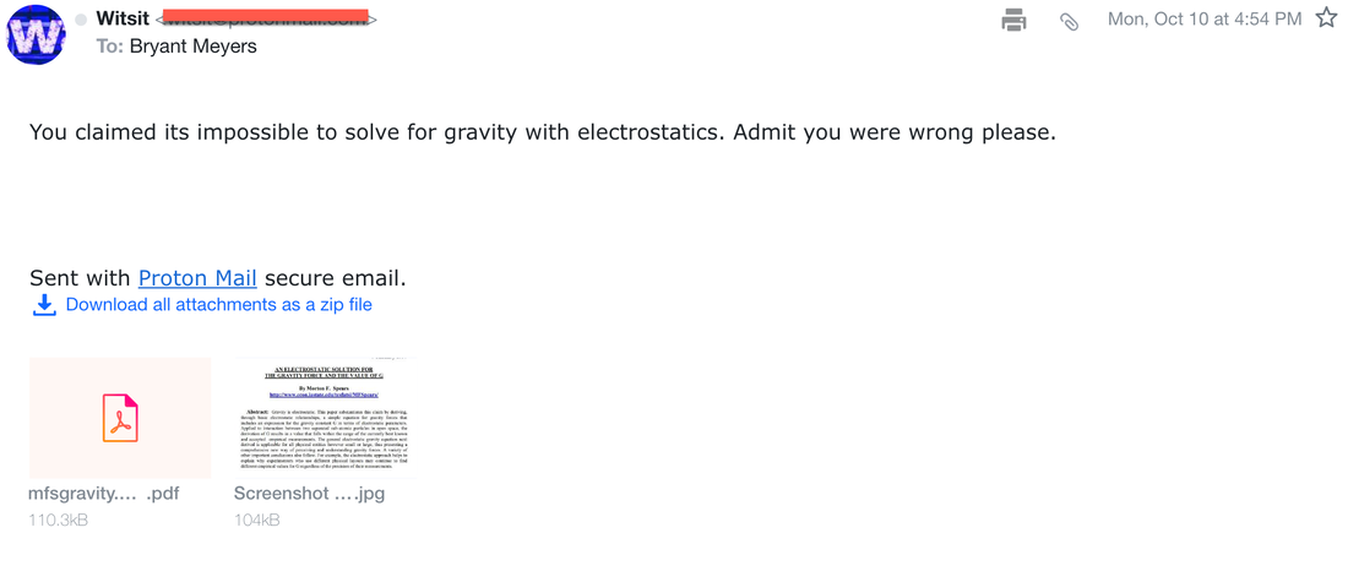
Actually the PUBLISHED research from rainfall and gravity models it uses Mass attracts mass. Not electrostatics.
https://www.researchgate.net/figure/Rainfall-and-gravity-as-a-function-of-time-through-two-rainy-seasons-at-The-Geysers_fig13_224490308
https://www.researchgate.net/figure/Rainfall-and-gravity-as-a-function-of-time-through-two-rainy-seasons-at-The-Geysers_fig13_224490308
The symbols U(1), SU(2) and SU(3) refer to specific symmetry groups. These are symmetry groups that characterize the particle fields that constitute the Standard Model of particle physics.
Let me start with the simplest, U(1). Imagine, for a moment, a quantity that is measured by a vector in two dimensional space. Such a vector has a magnitude and a direction, of course. But imagine that you find out that actual, measurable physical quantities, things that we can read off our instruments, depend only on the magnitudes of these vectors, and not their direction. In other words, if someone rotated the vectors by some amount without changing their lengths, we would be none the wiser.
Such a vector field is said to have U(1) gauge symmetry. U(1) specifically refers to rotations in a plane. That plane is not a physical, geometric plane, mind you. In this case, it is the abstract, Gaussian plane of complex numbers. But specifically the electromagnetic field exhibits this symmery: The quantities that characterize it can be rotated in this two-dimensional plane without any effect whatsoever on things that we measure, such as the electric and the magnetic field.
This U(1) symmetry is the simplest and the easiest to explain. Next comes SU(2). This does not have an easy visualization though it is, indirectly, connected to rotations in three dimensions. But again, this is not a physical, geometric three dimensional space. Rather, the three parameters of this abstract rotation correspond to a triplet of fields: The W+ and W- bosons and the Z boson of the weak interaction. This connection, too, is indirect. These bosons are massive, and massive particles break the gauge symmetry. However, the symmetry breaking has its own mechanism, and we can determine what the fields must be like before that mechanism kicks in. This “unbroken” symmetry is actually characterized by the product group SU(2)×U(1) that combines the two symmetries.
Similarly, the strong interaction and its vector bosons, the gluons, obey an even more complicated symmetry group (though one that is, for a change, unbroken, as gluons remain massless). This is SU(3), sometimes written as SU(3)c, the ‘c’ signifying that this refers to the “color” charge of the strong interaction.
And there you have it: the complete gauge group of the Standard Model of particle physics is SU(3)×SU(2)×U(1).
As to the significance of these gauge groups: Apart from the symmetry breaking aspect that makes it possible for many particles to become massive, they provide a mechanism for the fields to interact with each other and also play a key role in making the theory “renormalizable”, which is to say, amenable to a mathematical procedure that gets rid of unwanted infinities and yields finite-valued predictions that can be tested against accelerator experiments.
Let me start with the simplest, U(1). Imagine, for a moment, a quantity that is measured by a vector in two dimensional space. Such a vector has a magnitude and a direction, of course. But imagine that you find out that actual, measurable physical quantities, things that we can read off our instruments, depend only on the magnitudes of these vectors, and not their direction. In other words, if someone rotated the vectors by some amount without changing their lengths, we would be none the wiser.
Such a vector field is said to have U(1) gauge symmetry. U(1) specifically refers to rotations in a plane. That plane is not a physical, geometric plane, mind you. In this case, it is the abstract, Gaussian plane of complex numbers. But specifically the electromagnetic field exhibits this symmery: The quantities that characterize it can be rotated in this two-dimensional plane without any effect whatsoever on things that we measure, such as the electric and the magnetic field.
This U(1) symmetry is the simplest and the easiest to explain. Next comes SU(2). This does not have an easy visualization though it is, indirectly, connected to rotations in three dimensions. But again, this is not a physical, geometric three dimensional space. Rather, the three parameters of this abstract rotation correspond to a triplet of fields: The W+ and W- bosons and the Z boson of the weak interaction. This connection, too, is indirect. These bosons are massive, and massive particles break the gauge symmetry. However, the symmetry breaking has its own mechanism, and we can determine what the fields must be like before that mechanism kicks in. This “unbroken” symmetry is actually characterized by the product group SU(2)×U(1) that combines the two symmetries.
Similarly, the strong interaction and its vector bosons, the gluons, obey an even more complicated symmetry group (though one that is, for a change, unbroken, as gluons remain massless). This is SU(3), sometimes written as SU(3)c, the ‘c’ signifying that this refers to the “color” charge of the strong interaction.
And there you have it: the complete gauge group of the Standard Model of particle physics is SU(3)×SU(2)×U(1).
As to the significance of these gauge groups: Apart from the symmetry breaking aspect that makes it possible for many particles to become massive, they provide a mechanism for the fields to interact with each other and also play a key role in making the theory “renormalizable”, which is to say, amenable to a mathematical procedure that gets rid of unwanted infinities and yields finite-valued predictions that can be tested against accelerator experiments.