SEEING Earth Curvature
The Bonneville Salt Flats
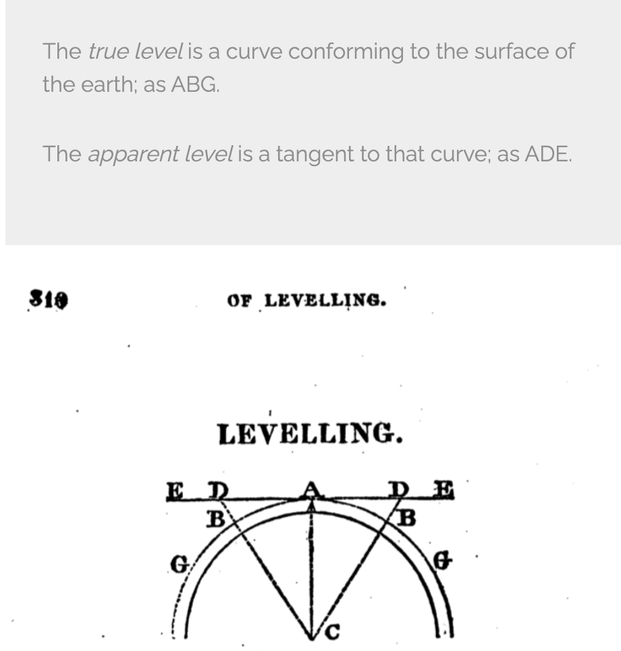
The true level is a curve conforming to the surface of the earth.
-A Treatise on Practical Surveying
The Bonneville Salt Flats
The true level is a curve conforming to the surface of the earth.
-A Treatise on Practical Surveying
The Bonneville Salt Flats is one of the most unique natural features in Utah, stretching over 30,000 acres.
The Bonneville Salt Flats and the Great Salt Lake are remnants of ancient Lake Bonneville. Wind and water combine to create the flat surface of salt. Each winter, a shallow layer of standing water floods the surface of the salt flats. During spring and summer, the water slowly evaporates while winds smooth the surface into a vast, nearly perfect flat plain.
The salt surface contains potassium, magnesium lithium and sodium chloride (common table salt).
The Bonneville Salt Flats and the Great Salt Lake are remnants of ancient Lake Bonneville. Wind and water combine to create the flat surface of salt. Each winter, a shallow layer of standing water floods the surface of the salt flats. During spring and summer, the water slowly evaporates while winds smooth the surface into a vast, nearly perfect flat plain.
The salt surface contains potassium, magnesium lithium and sodium chloride (common table salt).
“Looks flat to me”
Our eyes are not sensitive measuring devices. We are incapable of distinguishing 1 degree of arc from a straight line.
Our eyes are not sensitive measuring devices. We are incapable of distinguishing 1 degree of arc from a straight line.
Flat-Earthers incorrectly claim that salt flats are perfectly flat and use them to “prove” a flat Earth. In reality, salt flats form a curve following Earth’s curvature, like the ocean’s surface. No seen from the ground they do "look" flat. But here is a problem flat earthers never seem to GET.
Watch this footage here and it seems like the flats are well FLAT. However
Watch this footage here and it seems like the flats are well FLAT. However
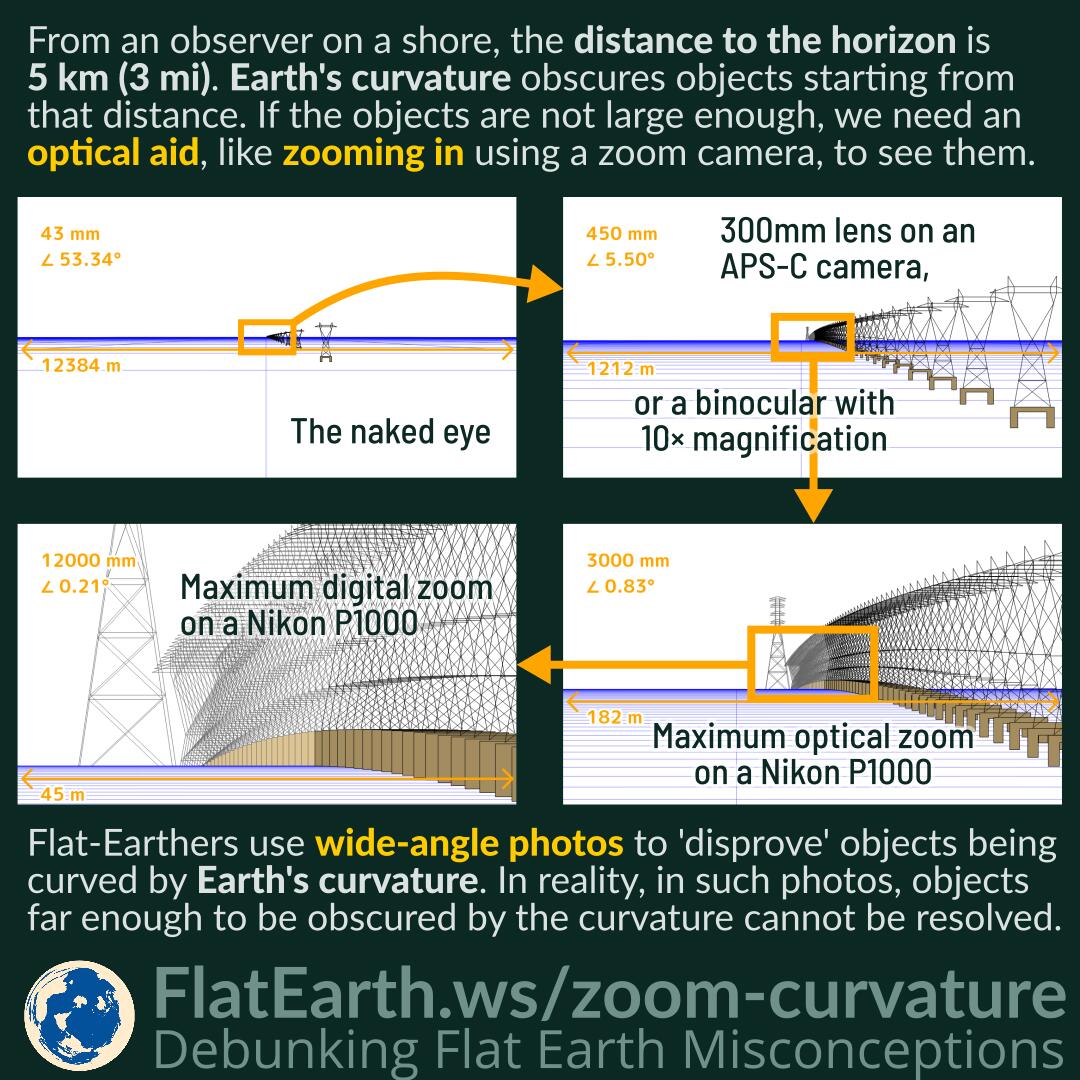
If the Earth is a Sphere, it should be curving away from us.
We can see this curve even close to sea level with the help of the right vantage point, good conditions and telescopic camera.
The Salt Flats in Utah are a great place to test if “level” means “curved” matching the definition, or if it means “flat” as some people have tried to assert. The salt flats are formed by water depositing salt when it evaporates. This means the surface is “level”.
We can see this curve even close to sea level with the help of the right vantage point, good conditions and telescopic camera.
The Salt Flats in Utah are a great place to test if “level” means “curved” matching the definition, or if it means “flat” as some people have tried to assert. The salt flats are formed by water depositing salt when it evaporates. This means the surface is “level”.
Interstate 80 traverses the Bonneville Salt Flat, Utah, in a practically straight segment. From the hilly terrain to the west of the highway, we can observe the highway’s curve following Earth’s curvature using a long-zoom camera.
And when they are doing speed runs, the officials can’t see the entire length of the track from the starting point. That is why they’ve got towers set up along its entire length so they can see the cars running constantly in case there’s an accident.
Objection #1 - Its Fake
Objection #2 - That is Just a Hill
60 nm is 1 degree of curvature, and that stretch is 50 miles, how much curvature is there?
Distance 47 miles (run). Elevation difference 53 feet (rise). Slope .02%. Not a hill.
The roads built across 47 miles of the Salt Flats have a 53 feet of elevation change. This is a slope of 0.02%. It’s not a hill. The Image is compressed perspective from a telescopic lens (more on this in a moment)
60 nm is 1 degree of curvature, and that stretch is 50 miles, how much curvature is there?
Distance 47 miles (run). Elevation difference 53 feet (rise). Slope .02%. Not a hill.
The roads built across 47 miles of the Salt Flats have a 53 feet of elevation change. This is a slope of 0.02%. It’s not a hill. The Image is compressed perspective from a telescopic lens (more on this in a moment)
Objection #3 You Can't See Curvature Near Sea Level
The horizon appears flat because the curvature is too small when observed from near the Earth’s surface. However, in some cases, we can exaggerate the curve by taking photographs or videos of the horizon and then magnifying the results.
Two Scenarios
1) Use a wide Angle Lens to Capture Side to Side Curve and Compress
2) Use a Telescopic Lens to Capture forward - back curvature.
The horizon appears flat because the curvature is too small when observed from near the Earth’s surface. However, in some cases, we can exaggerate the curve by taking photographs or videos of the horizon and then magnifying the results.
Two Scenarios
1) Use a wide Angle Lens to Capture Side to Side Curve and Compress
2) Use a Telescopic Lens to Capture forward - back curvature.
At the top of Wendover Blvd, there's a place to turn out just by the water basin, the time lapse and 2 other videos are from there. Then I climbed up a big hill (Wendover Viewpoint on Google Earth) and that's where I got the shot that's more straight on. I believe it's roughly 900ft higher than the salt bed. ~ David Cook (Don't Stop Motion)
People have asked why the curve is so apparent in one direction, but not in the other. The answer is compressed perspective. Here's a physical example:
Right To Left Curve at Low Elevation - Compressed left to right.
The images were taken on the island of Ibiza at 39° 2′ 30.24″ N, 1° 18′ 47.388″ E at an elevation of 603 feet. Feel free to download the image and look at the EXIF information.
We can see the straight edges are straight and the horizon is curved. Solid evidence of left to right curve.
I challenge honest flat earthers to have the courage to reproduce this experiment. Find a place 500 feet or higher where you can easily see the horizon. Pick a day with minimal weather variances. Get two straight edges such as 8-foot metal spirit levels. Place uniform spacers between them and strap or tape them firmly together. Set this up in a way that makes it easy to adjust the straight edges so they can be lined up with the horizon. Use a good camera and take a photo from a good distance so both the straight edges and the horizon are in focus. Take many photos. Then compare the straight edge to the horizon.
I challenge honest flat earthers to have the courage to reproduce this experiment. Find a place 500 feet or higher where you can easily see the horizon. Pick a day with minimal weather variances. Get two straight edges such as 8-foot metal spirit levels. Place uniform spacers between them and strap or tape them firmly together. Set this up in a way that makes it easy to adjust the straight edges so they can be lined up with the horizon. Use a good camera and take a photo from a good distance so both the straight edges and the horizon are in focus. Take many photos. Then compare the straight edge to the horizon.
https://www.tiktok.com/@arizonalandsurveyor/video/7260290287287749930?_r=1&_t=8fYFZsEw6Qs
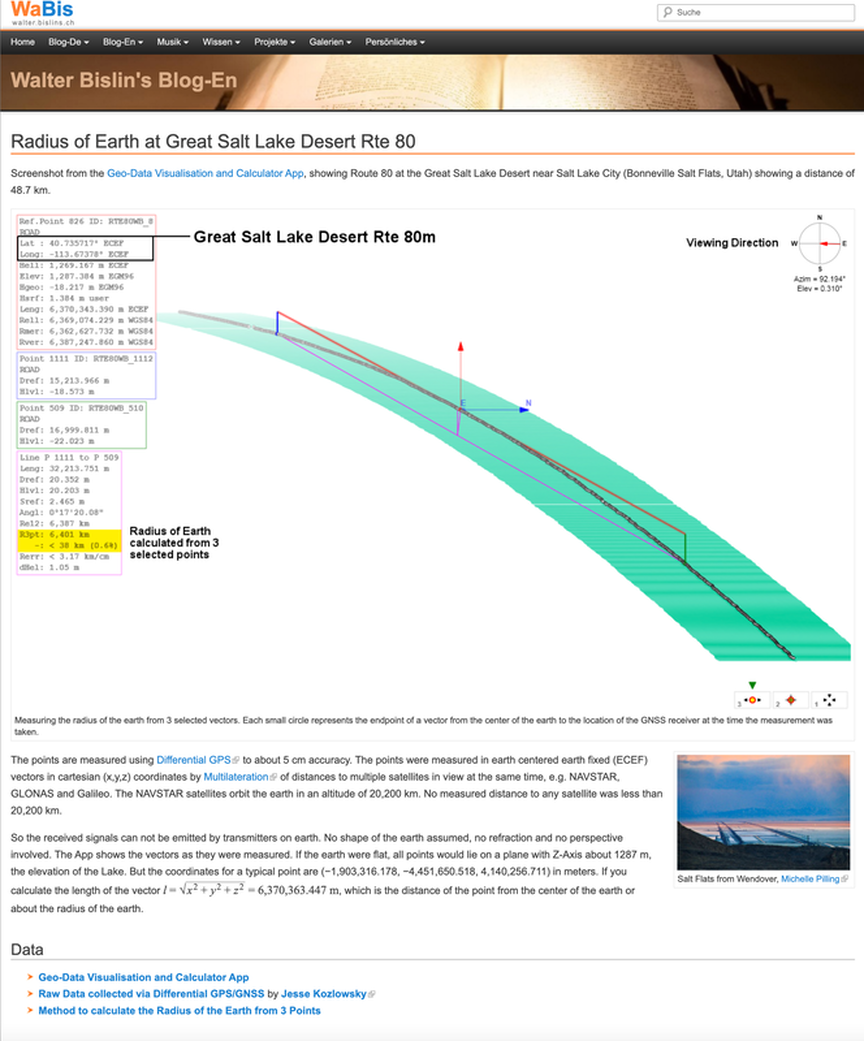
GNSS (Global Navigation Satellite System) Of Rte 80 For 40 Miles Across The Bonneville Salt Flats In Utah; Video by Jesse Kozlowsky
The points are measured using Differential GPS to about 5 cm accuracy. The points were measured in earth centered earth fixed (ECEF) vectors in cartesian (x,y,z) coordinates by Multilateration of distances to multiple satellites in view at the same time, e.g. NAVSTAR, GLONAS and Galileo. The NAVSTAR satellites orbit the earth in an altitude of 20,200 km. No measured distance to any satellite was less than 20,200 km.
So the received signals can not be emitted by transmitters on earth. No shape of the earth assumed, no refraction and no perspective involved. The App shows the vectors as they were measured. If the earth were flat, all points would lie on a plane with Z-Axis about 1287 m, the elevation of the Lake. But the coordinates for a typical point are (−1,903,316.178, −4,451,650.518, 4,140,256.711) in meters. If you calculate the length of the vector l = √x2 + y2 + z2 = 6,370,363.447 m, which is the distance of the point from the center of the earth or about the radius of the earth.
So the received signals can not be emitted by transmitters on earth. No shape of the earth assumed, no refraction and no perspective involved. The App shows the vectors as they were measured. If the earth were flat, all points would lie on a plane with Z-Axis about 1287 m, the elevation of the Lake. But the coordinates for a typical point are (−1,903,316.178, −4,451,650.518, 4,140,256.711) in meters. If you calculate the length of the vector l = √x2 + y2 + z2 = 6,370,363.447 m, which is the distance of the point from the center of the earth or about the radius of the earth.
Curve of the earth visualized and measured
1) PHOTOS - Whole Earth
Whole Earth - Apollo, Artemis, Himawari/GOES, DSCOVR
1) PHOTOS - Whole Earth
Whole Earth - Apollo, Artemis, Himawari/GOES, DSCOVR
2) PHOTOS - High Altitude - MAGE2, High Altitude Rocket, ISS
Shows Left to Right Curve at a High Altitude
Shows Left to Right Curve at a High Altitude
M-A-G-E 1 & 2
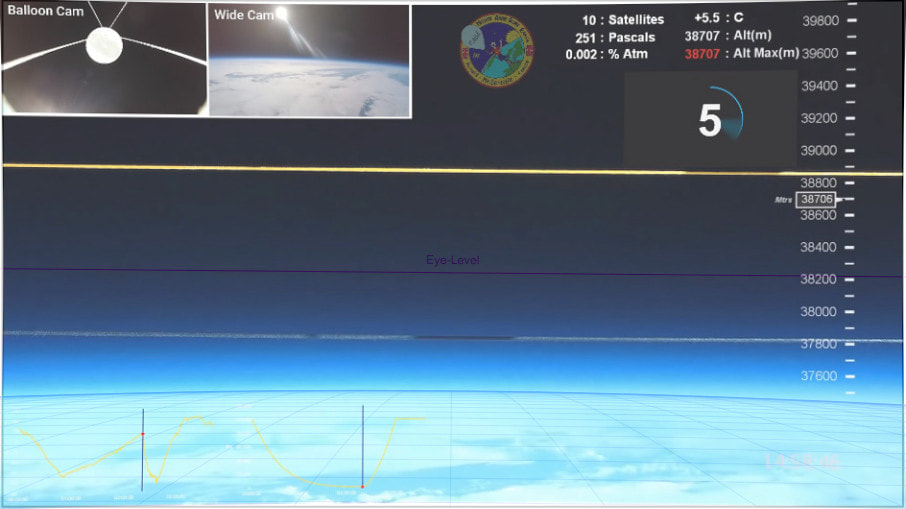
Mr Sensible conducted a high altitude ballon experiment that contained 3 cameras, a pressure and a temperature sensor and a GPS device. The goal was to record pressure, temperature and altitude, as well as to show the curvature of the earth to an altitude up to 39,000 m. The altitude was almost reached.
The Front Camera with the 2 strings in the field of view was a Firefly 8SE 90°, set to a diagonal field of view of 51.6°, see Measuring the Field of View of the Front Camera. This camera has only a slight barrel distortion, which Walter Bislin corrected with a Lightroom setting of 8 of 100, so that the 2 strings are straight and the image below shows the undistorted reality.
No Fisheye, slight barrel distortion EASILY corrected (As walter has done)
Field of View Narrow (curve would be more obvious in a larger field of view
Not only is horizon curved as expected on the globe but it drops from eye level 6.3 percent
MAGE 2 on youtube and MAGE 3 coming soon
Then Walter imported the image into his Curvature App, set the observer altitude to 38,706 m as indicated in the video and set the field of view to 51.6° as measured from the camera.
http://walter.bislins.ch/bloge/index.asp?page=M%2EA%2EG%2EE%2E+%2D+Mission+Above+Globe+Earth%2C+Image+Analysis
Mr Sensible conducted a high altitude ballon experiment that contained 3 cameras, a pressure and a temperature sensor and a GPS device. The goal was to record pressure, temperature and altitude, as well as to show the curvature of the earth to an altitude up to 39,000 m. The altitude was almost reached.
The Front Camera with the 2 strings in the field of view was a Firefly 8SE 90°, set to a diagonal field of view of 51.6°, see Measuring the Field of View of the Front Camera. This camera has only a slight barrel distortion, which Walter Bislin corrected with a Lightroom setting of 8 of 100, so that the 2 strings are straight and the image below shows the undistorted reality.
No Fisheye, slight barrel distortion EASILY corrected (As walter has done)
Field of View Narrow (curve would be more obvious in a larger field of view
Not only is horizon curved as expected on the globe but it drops from eye level 6.3 percent
MAGE 2 on youtube and MAGE 3 coming soon
Then Walter imported the image into his Curvature App, set the observer altitude to 38,706 m as indicated in the video and set the field of view to 51.6° as measured from the camera.
http://walter.bislins.ch/bloge/index.asp?page=M%2EA%2EG%2EE%2E+%2D+Mission+Above+Globe+Earth%2C+Image+Analysis
3) Horizon DIP
If the earth is a sphere then the horizon must drop from the apparent level, sometimes called “eye level”.
This is predicted to be very slight so any measurements must be capable of more precision than the predicted dip.
If the earth is a sphere then the horizon must drop from the apparent level, sometimes called “eye level”.
This is predicted to be very slight so any measurements must be capable of more precision than the predicted dip.
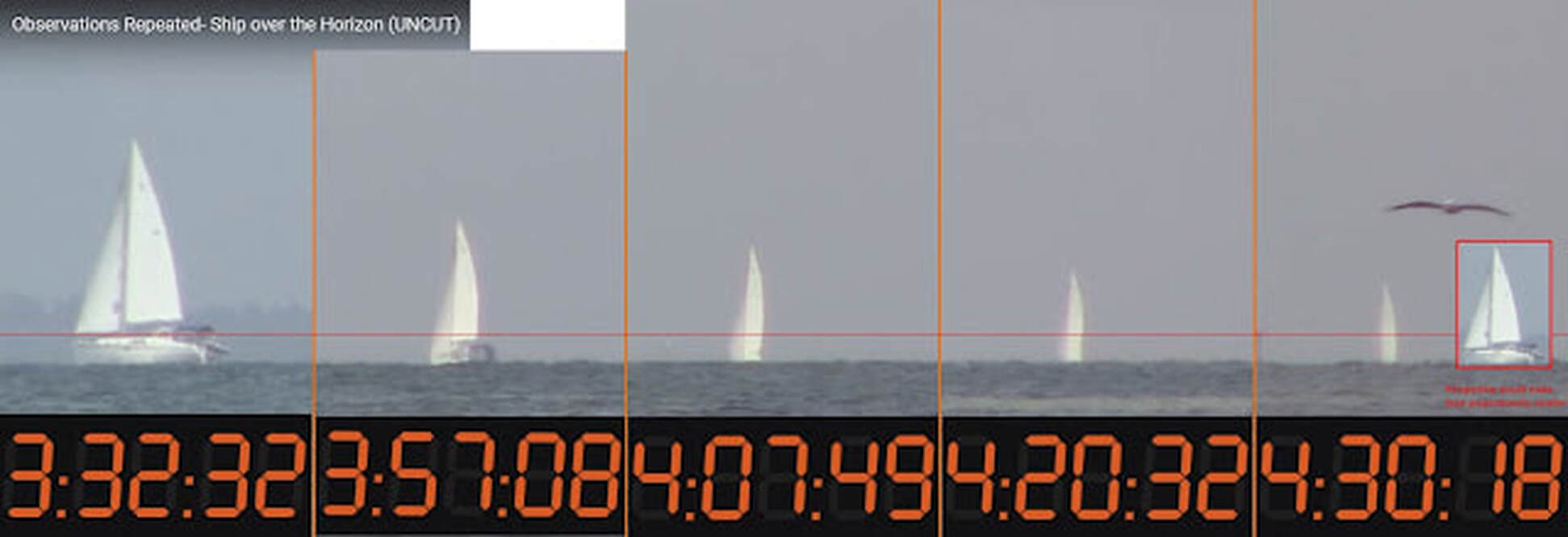
4) Forward to Back Curvature - This Video and Ships Disappearing Bottom up over the Horizon!
5) Measured Curvature - NOW GNSS Surveying Available in Addition to Traditional Surveying
If the earth is a sphere vertical lines must diverge.This is predicted to be very slight so any measurements must be capable of more precision than the predicted divergence.
- Baron Rutledge, measured reciprocal zenith angles in a video, plumb lines diverge.
- The Maine Surveyor, a licensed geodetic surveyor used two theodolites to precisely test for the divergence of vertical lines.
- Jesse Kozlowski, a licensed geodetic surveyor measured the divergence of plumb lines over one mile.
- Jesse Kozlowski also measured the vertical drop over a still and level lake: